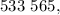 которая должна выражать дату (в каком-то неизвестном представлении).
которая должна выражать дату (в каком-то неизвестном представлении).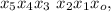


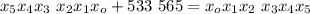 ;
;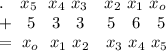

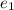 – возможная добавочная единица, уходящая из первого
– возможная добавочная единица, уходящая из первого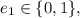
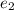 – возможная добавочная единица, уходящая из второго
– возможная добавочная единица, уходящая из второго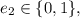
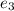 – возможная добавочная единица,
– возможная добавочная единица,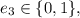
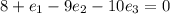 ;
;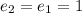 и при
и при  ;
;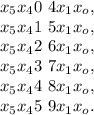
 поскольку
поскольку 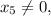 так как с этой цифры начинается разностное число.
так как с этой цифры начинается разностное число. поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.
поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.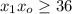 .
.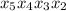 .
.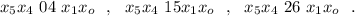
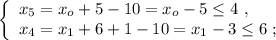

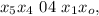
 может играть роль апреля.
может играть роль апреля.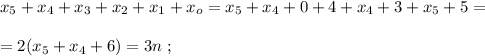
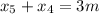 ;
;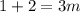 ;
;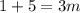 ;
;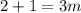 ;
; ;
;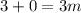 ;
;
 – дата 12/04/56 г.
– дата 12/04/56 г. – дата 15/04/86 г.
– дата 15/04/86 г.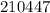 – дата 21/04/47 г.
– дата 21/04/47 г.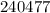 – дата 24/04/77 г.
– дата 24/04/77 г.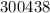 – дата 24/04/38 г.
– дата 24/04/38 г.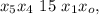
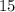 может играть только роль числа месяца (дня).
может играть только роль числа месяца (дня).
 ;
;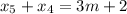 ;
;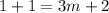 ;
;
 – дата 11/15/46 г.
– дата 11/15/46 г.

х = 32, у = 29.
Объяснение:
Записываем условие:
x - y = 3
x^2 - y^2 = 183
Выражаем y через х из первого уравнения.
y = x - 3
Заменяем y во втором уравнении.
x^2 - (x - 3)^2 = 183
Раскрываем x - 3 по правилу сокращенного умножения
(a - b)^2 = a^2 - 2ab + b^2
(x - 3)^2 = x^2 - 6x + 9
Записываем все в одно уравнение:
x^2 - (x^2 - 6x + 9) = 183
Раскрываем скобки, меняя знаки.
x^2 - x^2 + 6x - 9 = 183
6x - 9 = 183
6x = 192
x = 192/6 = 32
Следовательно y = x - 3 = 32 - 3 = 29.
Проверяем:
32 - 29 = 3
32^2 = 1024; 29^2 = 841; 1024 - 841 = 183
Все верно.
Otvet: 10