62°
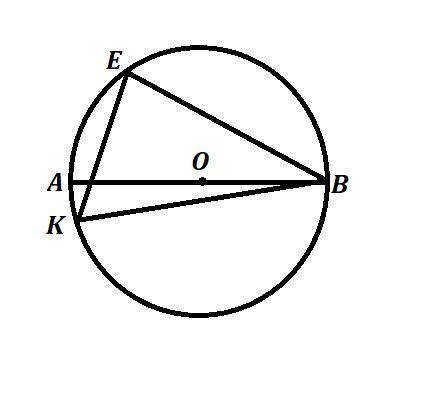
Объяснение:Вписанный угол - угол, у которого вершина находится на окружности, а его стороны пересекают окружность.Вписанный угол измеряется половиной дуги, на которую опирается.∠ABE - вписанный и опирается на ∪AE ⇒ ∪AE = ∠ABE * 2 = 21° * 2 = 42°
∠EBK - вписанный и опирается на ∪EK ⇒ ∪EK = ∠EBK * 2 = 49° * 2 = 98°
⇒ ∪AK = ∪EK - ∪AE = 98° - 42° = 56°
∪AB = 180°, так как AB - диаметр данной окружности, по условию.
⇒ ∪KB = ∪AB - ∪AK = 180° - 56° = 124°
∠BEK - вписанный и опирается на ∪KB ⇒ ∠BEK = ∪KB : 2 = 124° : 2 = 62°
Пусть х - скорость парохода, у - скорость течения.
Тогда из условия имеем систему:
100/(х+у) + 64/(х-у) = 9 100x - 100y + 64x + 64y = 9(x^2-y^2)
80/(х+у) + 80/(х-у) = 9 80х-80у+ 80х + 80у = 9(x^2-y^2)
164x - 36y = 160x x = 9y
Тогда: 1440y = 720y^2 y^2-2y=0 y = 2 x = 18
ответ: 18 км/ч; 2 км/ч.