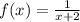


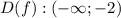 ∪
∪
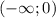 ∪
∪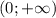

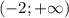
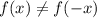
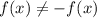

1) графический метод - см. вложение
прямые пересекаются в точке с координатами (3;2), значит х = 3 y = 2
2) метод подстановки
-x+2y=4,
7x-3y=5;
х = 2y - 4,
7(2y - 4) - 3y = 5;
14y - 28 - 3y = 5
11y = 33
y = 3
x = 2*3 - 4 = 2
y = 3, x = 2
3) метод алгебраического сложения
3x-2y=64
3x+7y=-8
вычтем из 1ого уравнение 2ое :
(3x - 2y) - (3x +7y) = 64 - (-8)
-9y = 72
y = -8
Подставим полученное значение y в любое из 2х уравнений системы:
3х -2*(-8) = 64
3х = 48
х = 16
т.е. х = 16 y = -8
4) точка пересечения y=-7/8x + 17 и y = -3/5х-16:
-7/8x + 17 = -3/5х-16
7/8х - 3/5х = 33
11x/40 = 33
x = 120
y = (-7/8)*120 + 17 = -88
график уравнения y+px=0 пройдет через точку пересечения прямях (120;-88)
-88 +120p = 0
p = 88/120 = 11/15

3x^2-2x+9x-6≥2x^2+12
3x^2+7x-6-2x^2-12≥0
x^2+7x-18≥0
Нули:(по теореме Виета)
x1=2
x2=-9
Знаки интервалов:
- 9 2 >
+ - +
ответ: x∈(-∞; -9] ∪ [2; +∞)