Объяснение:
Разложить число на простые множители значит записать число как произведение простых чисел .
Простым числом называют натуральное число , делящееся только на себя и на единицу. Составным числом называют число, имеющее больше двух различных делителей Например, числа 2,3,5,7, – простые, а числа 6(2*3),8(2*4),9(3*3) – составные.
Число 388 , оканчивается на 8 значит делится на 2
388:2=194, оканчивается на четное , значит также делится на 2
194 :2= 97 ,вспомним признаки делимости на 3 и 9 , число делится если сумма его цифр делится на 3 или 9.На четыре делится если 2 его последние цифры нули или образуют число которое делится на 4, На пять делится если число оканчивается на 5 или 0.осталось число 6 и 8. На 6 делится если одновременно делится на 2 и 3 , и число делится на 8, если три его последние цифры - нули или образуют число, которое делится на 8.
97=9+7=16, ни на одно число не делится, кроме 1 и самого себя значит 97 это простое число.
388=2*2*97
Число 2520
2520:2= 1260 ( признак делимости на 2)
1260:2=630 ( признак делимости на 2)
630:2=315 ( признак делимости на 5)
315:5=63 ( признак делимости на 3 и 9; 6+3=9 делится и на 3 и на 9
63:3=21 (2+1=3, признак делимости на 3 )
21:3=7 ( неделимое, простое число)
2520 = 2*2*2*3*3*5*7
2) Чтобы обратить обыкновенную дробь в десятичную, нужно числитель разделить на знаменатель.
3 2/5=17/5=17:5=3,4 мы получили конечную десятичную дробь, поскольку в знаменателе обыкновенной дроби стоит 5 ( получить конечную десятичную дробь можно если знаменатель обыкновенной дроби содержит простые множители 2 и 5)
43/30=43:30=1,4 33333… = 1,4(3), поскольку знаменатель обыкновенной дроби содержит кроме 2 и 5 еще 3, то она не может быть представлена конечной десятичной дробью.
1)Найдите девятый член последовательности
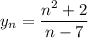

2) Найдите пятый член последовательности заданной рекуррентным у1 = ½, yₙ=2*y₍ₙ₋₁₎
y₂=2*1/2=1; y₃=2*1=2; y₄=2*2=4; y₅=2*4=8
3) Подберите формулу n- го члена последовательности - 2/2; 4/5; - 6/8; 8/11; -10/14;

проверка:
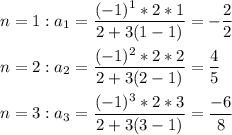
4) Сколько членов последовательности 3, 6, 9, 12,….меньше числа 95
аₙ=а₁+3(n-1)
aₙ<95
a₁+3(n-1)<95
3+3n-3<95
3n<95
n<31.(6)
n=31
проверим: a₃₁=3+3(31-1)=3+3*30=93
Значит 31 член меньше 95
5) у₁ = 2, у₂ = 1, уₙ = 2y₍ₙ₋₂₎+3y₍ₙ₋₁₎ (n = 3,4,5,…).Найдите n, если известно, что уₙ = 83.
тут можно просто решить находя слены этой последовательности
y₁=2
y₂=1
y₃=2*2+3*1=4+3=7
y₄=2*1+3*7=2+21=23
y₅=2*7+3*23=14+69=83
N=5