91
Объяснение:
Какое наименьшее количество различных трехзначных чисел нужно взять, чтобы среди них наверняка было бы одно число, оканчивающееся НЕ на нуль - на одно больше чем количество различных трехзначных чисел оканчивающееся на нуль
Найдем количество различных трехзначных чисел оканчивающееся на нуль, последняя цифра 0 (1 вариант выбора), первая любая цифра от 1 до 9 (9 вариантов выбора), вторая - любая цифра от 0 до 9 (10 вариантов выбора), по правилу умножения событий, получаем что всего таких чисел 9*10*1=90
а значит нужно 91 число (90+1=91)
A)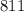 
Б)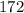 
Объяснение:
A)Трехзначные числа со средней цифрой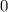 
имеют вид:
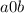
Цифра 
меняется от 
до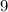 
, а цифра 
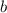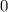от до .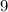
Таким образом, общее число чисел со средней цифрой 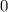равно: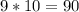 
Общее число трехзначных чисел :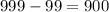 
Тогда, число трехзначных чисел со средней цифрой отличной от нуля:
.
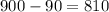Таким образом, чтобы среди взятых трехзначных чисел, наверняка было число со средней цифрой 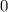, нужно взять: 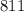трехзначных чисел.
Б) Определим общее число трехзначных чисел без нулей в десятичной записи.
На каждом из разрядов могут стоять цифры от до 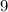(все кроме )
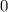Тогда, общее число таких трехзначных чисел: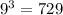 
Откуда, число трехзначных чисел содержащих ноль: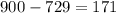 
Как видим, нужно взять как минимум : 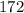трехзначных числа, чтобы среди них обязательно было число без нулей в десятичной записи.
Підставимо і отримаємо 3х=6 --- х=2
маємо точку А (2;0)
При перетині з віссю Оу х=0
Аналогічно -2у=6 -- у=-3
Маємо точку В (0;-3)