Задача: Сумма катетов прямоугольного треуольника равна 24 см. Найти длины катетов этого треугольника, при которых площадь треугольника будет наибольшей.
Пусть один катет будет x cm, тогда второй — 24−x cm. составим уравнение для вычисления площади прямоугольного т-ка, где x — независимая переменная, S — зависимая переменная:
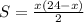
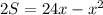
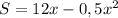
Графиком данной функции является парабола.
Определим вершину параболы, построим график функции S(x):
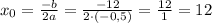
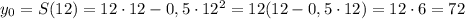
Ордината вершины параболы — и есть максимальная площадь треугольника. Абсцисса вершины — значение, которое принимает независимая переменная, то есть один из катетов прямоугольного треугольника, который мы обозначили за x.
Из графика видно, что длины катетов треугольника будут равны, и равны абсциссе вершины параболы.
Или выведем аналитически:
если один катет x = 12 cm, тогда второй 24−x = 24−12 = 12 cm
ответ: Катеты треугольника должны быть равны 12 и 12 см.
Максимальная площадь равна 72 см².
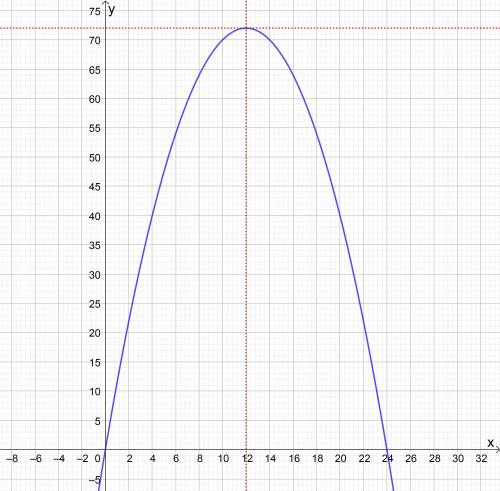
sin²(x) - 2 (a - 3) sin(x) + a² - 6a + 5 = 0 не имеет решений ?
Замена : t =sinx | t | ≤ 1
t² - 2 (a - 3)*t + a²- 6a + 5 = 0
D/4 =(a -3)² -(a²- 6a + 5) =a²- 6a + 9 -a²+ 6a - 5 =4 =2² .
⇒( квадратное уравнение имеет два различных действительных корня)
t₁=a-3 -2 =a -5 ;
t₂ =a-3+2 =a -1.
Исх. уравнение не имеет решение, если не удовлетворяется | t | ≤ 1,т.е.
если :
а) { a - 5 < -1 ; a - 1 < -1 .⇔ { a < 4 ; a <0. ⇒ a < 0 , иначе a ∈( -∞; 0).
б). { a - 5 < - 1 ; a - 1 > 1.⇔ { a < 4 ; a >2. ⇒ a ∈( 2 ; 4 )
г). { a - 5 > 1 ; a - 1 > 1 .⇔ { a > 4 ; a >2. ⇒ a ∈( 4 ; ∞ ).
д) { a - 5 > 1 ; a - 1 < - 1. * * * невозможно т.к. a - 1 > a -5 * * *
{ a > 6 ; a < 0 . ⇒ a∈ ∅.
ответ : a ∈( -∞; 0) ∪ (2 ;4) ∪(4 ; ∞)