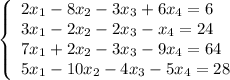
Для удобства вычислений, поменяем местами строчки системы ЛНУ .

1 строку * 7 - 5*2 строку ; 1стр*3 - 5*3стр ; 1стр*2-5*4стр
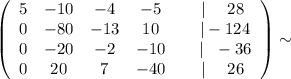
2стр - 4*3стр ; 3 стр + 4стр
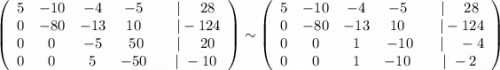
Для перехода к последней матрице разделили 3 строку на (-5) , а 4 строку на 5 .
Ранг матрицы системы ( та, что записана до вертикальной черты, размером 4×4 ), равен 3, так как две последние строки равны, а значит одну из строк можно вычеркнуть. Ранг расширенной матрицы ( та, что записана без учёта вертикальной черты, размером 4×5 ) равен 4, так как2 последние строки различны. Ранги указанных матриц НЕ равны, то есть условия теоремы Кронекера-Капелли не выполняются, значит система НЕ ИМЕЕТ РЕШЕНИЙ, то есть система НЕСОВМЕСТНА .
Общее решение системы можно было бы записать лишь в случае, если бы система была совместна и не определена .

Вариантов перестановки 6*5*4*3*2=720 (вариантов)
Если не знать формулу, то считаем так:
Вариантов для 1 урока 6.. Далее к каждому из них: 5 вариантов для 2 урока. (т.е. например, 1 алгебра , тогда любой из 5 оставшихся - второй, и т.д. с 1 руским, 1 литературой и т.д. ,т.е. это уже 6*5=30 вариантов, ну и дальше к каждому из выбранных вторых- 4 оставшихся варианта для 3 урока , 30*4=120, к каждому из этих 120 , 3 варианта для 4 урока 120*3=360, 2 варианта для 5 урока 360*2=720 и шестой уже без вариантов.