Мастер должен был изготовить 72 детали а ученик 64 детали изготовляя в час на 4 детали больше чем ученик мастер выполнил заказ на 2 часа раньше сколько деталей изготовлял в час мастер и сколько ученик

👇

Ответ:

ната555555

20.12.2020

Пусть производительность труда ученика х дет/час, а мастера х+4,
тогда ученик выполнит работу за 64/х, а мастер - 72/(х+4).

Cоставим и решим уравнение
64/х - 72/ (х+4) = 2
64(х+4) - 72*х = 2*х*(х+4)
64х + 256 - 72х = 2х² + 8х
-8х + 256 - 2х² - 8х = 0
2х² + 16х - 256 = 0 / : 2
х² + 8х - 128 = 0
D = 64 + 512 = 576 = 24^2
x1 = ( - 8 + 24)/2 = 16/2 = 8
x2 = ( - 8 - 24)/2 = - 32/2 = - 16 не удовлетворяет условию задачи

Cледовательно, ученик в час изготавливает 8 деталей, а мастер 8+4= 12

4,6(44 оценок)

Открыть все ответы

Ответ:

chelovekchelovekov99

20.12.2020

Для геометрической прогрессии со знаменателем Q и первым членом B₁ верно следующее: Bₙ = Qⁿ⁻¹ * B₁, откуда Qⁿ⁻¹ = Bₙ : B₁ = 1024 : 2 = 512. Итак, отмечаем: Qⁿ⁻¹ = 512. Формула для суммы первых n членов прогрессии:

Sₙ = B₁(Qⁿ - 1)/(Q - 1) = B₁(Q * Qⁿ⁻¹ – 1) / (Q – 1) = 2*(512Q - 1) / (Q - 1) = 2046 ⇒

1024Q - 2 = 2046(Q - 1) ⇒ 1024Q - 2 = 2046Q - 2046 ⇒

2046Q - 1024Q = 2046 - 2 ⇒ 1022Q = 2044 ⇒ Q = 2044 : 1022, Q = 2.

Далее Qⁿ⁻¹ = 512 ⇒ 2ⁿ⁻¹ = 512 = 2⁹ ⇒ n - 1 = 9, откуда n = N = 10,

за N заново обозначили количество членов данной прогрессии

ответ: Q = 2, N = 10

Проверка: 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + 512 + 1024 = 2046

4,6(66 оценок)

Ответ:

linaaaa2Li

20.12.2020

Объяснение:

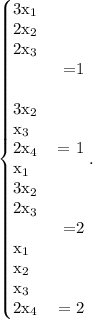
$\left\{\begin{array}{}3x_1&2x_2&2x_3& \ \ \ \ \ \ =1\\&3x_2&x_3&2x_4\ \ =1\\x_1&3x_2&2x_3&\ \ \ \ \ \ \ \ =2\\x_1&x_2&x_3&2x_4\ \ \ =2\end{array}\right..$

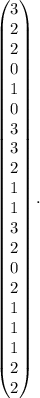
$\left(\begin{array}{}3&2&2&0&1\\0&3&3&2&1\\1&3&2&0&2\\ 1&1&1&2&2\end{array}\right).$

Поменяем местами 1-ю и 3-ю строки:

$\left(\begin{array}{}1&3&2&0&2\\0&3&3&2&1\\3&2&2&0&1\\ 1&1&1&2&2\end{array}\right).$

Вычитаем из 4-й строки 1-ю строку:

$\left(\begin{array}{}1&3&2&0&2\\0&3&3&2&1\\3&2&2&0&1\\ 0&-2&-1&2&0\end{array}\right).$

Вычитаем из 3-й строки 1-ю строку, умноженную на 3:

$\left(\begin{array}{}1&3&2&0&2\\0&3&3&2&1\\0&-7&-4&0&-5\\ 0&-2&-1&2&0\end{array}\right).$

Разделим 2-ю строку на 3:

$\left(\begin{array}{}1&3&2&0&2\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&-7&-4&0&-5\\ 0&-2&-1&2&0\end{array}\right).$

Суммируем 3-ю и 2-ю строку, умноженную на 7:

$\left(\begin{array}{}1&3&2&0&2\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&3&\frac{14}{3} &-\frac{8}{3} \\ 0&-2&-1&2&0\end{array}\right).$

Суммируем 1-ю и 2-ю строку, умноженную на -3:

$\left(\begin{array}{}1&0&-1&-2&1\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&3&\frac{14}{3} &-\frac{8}{3} \\ 0&-2&-1&2&0\end{array}\right).$

Суммируем 4-ю и 2-ю строку, умноженную на 2:

$\left(\begin{array}{}1&0&-1&-2&1\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&3&\frac{14}{3} &-\frac{8}{3} \\ 0&0&1&\frac{10}{3} &\frac{2}{3} \end{array}\right).$

Поменяем местами 4-ю и 3-ю строки:

$\left(\begin{array}{}1&0&-1&-2&1\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&3&\frac{14}{3} &-\frac{8}{3} \end{array}\right).\\$

Суммируем 3-ю и 1-ю строки:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&3&\frac{14}{3} &-\frac{8}{3} \end{array}\right).\\$

Суммируем 2-ю и 3-ю строку, умноженную на -1:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&3&\frac{14}{3} &-\frac{8}{3} \end{array}\right).\\$

Суммируем 4-ю и 3-ю строку, умноженную на -3:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&0&-\frac{16}{3} &-\frac{14}{3} \end{array}\right).\\$

Разделим 4-ю строку на -16/3:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&0&1 &\frac{7}{8} \end{array}\right).\\$

Суммируем 1-ю и 4-ю строку, умноженную на -4/3:

$\left(\begin{array}{}1&0&0&0 &\frac{1}{2} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&0&1 &\frac{7}{8} \end{array}\right).\\$