ОДЗ :
x² - 15 > 0
(x - √15)(x + √15) > 0
+ - +
__________₀______________₀__________
- √15 √15
/////////////////////// ////////////////////////
x ∈ (- ∞ ; - √15) ∪ (√15 ; + ∞)
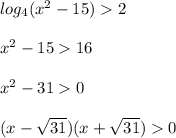
+ - +
____________₀___________₀___________
- √31 √31
////////////////////////// /////////////////////
ответ : x ∈ (- ∞ ; - √31) ∪ (√31 ; + ∞)
5050
Объяснение:
Карл Фридрих Гаусс заметил интересную закономерность, что если сгруппировать числа в пары получается алгоритм , благодаря которому можно быстро сложить числа от 1 до 100 .
Рассмотрим этот алгоритм :
1) Необходимо найти количество пар в ряду натуральных чисел. В нашем ряду 100 чисел , значит количество пар будет :
100 : 2 = 50 пар
2) Необходимо сложить первое и последнее число в ряду , в нашем случае это :
100 + 1 =101
3) Умножить сумму первого и последнего чисел в ряду на количество пар в ряду :
101 * 50= 5050
Получаем , что сумма чисел от 1 до 100 будет 5050
Сегодня этот алгоритм называется - правило Гаусса и широко применяется при устном счете
Перевіримо чи 0 являється членом прогресії.
В такому випадку, щоб знайти найменший за модулем член арифметичнох прогресії - знайдемо найбільший відємний, найменший додатній, порівнявши їх модулі знайдемо найменший за модулем член прогресії
найбільше натуральне яке задовільняє нерівність n=22, значить останній (в порядку зростання номера n) відємний член
наступний член прогресії - 23-й член (22+1=23) - буде найменший додатнім (так як переконались що 0 не буде членом, а послідовність являється зростаючою)
значить найменший член за модулем це 23-й член зі значенням 0.3