1) 3ˣ < 1 + 12·3⁻ˣ|·3ˣ; (3ˣ)² < 3ˣ + 12; (3ˣ)² - 3ˣ - 12 < 0; (3ˣ)² - 3ˣ - 12 = 0; - квадратное уравнение относительно 3ˣ, отсюда 3ˣ = 4 или 3ˣ = -3 - не имеет решений.
Рисунок во вложении
ответ: (-∞; log₃4)
2) 4·4ˣ < 7·2ˣ + 2; 4·4ˣ - 7·2ˣ - 2 < 0; 4·(2ˣ)² - 7·2ˣ - 2 = 0 - квадратное уравнение относительно 2ˣ, отсюда D = 49 + 32 = 81; √D = 9; 2ˣ = (7 + 9)/8 = 2 или 2ˣ = (7 - 9)/8 = -1/4 - не имеет решений.
Рисунок во вложении
ответ: (-∞; 1).
3) 9ˣ - 6·3ˣ - 27 = 0; (3ˣ)² - 6·3ˣ - 27 = 0; - квадратное уравнение относительно 3ˣ отсюда 3ˣ = 9; x = 2 или 3ˣ = -3 - не имеет решений.
ответ: 2.
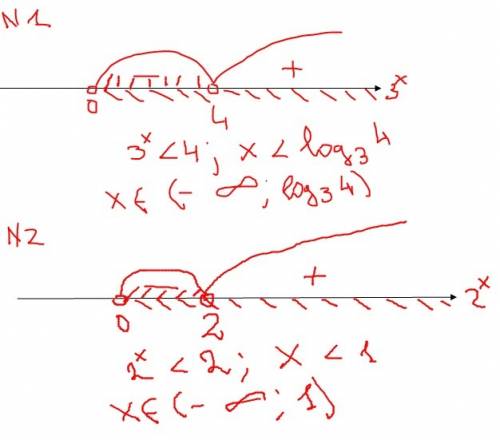
Надо взять 250 мл раствора концентрации 8% и 150 мл раствора концентрации 16%
Объяснение:
Для удобства вычислений переведём %-ты в десятичные дроби:
8%=8:100=0,08
16%=16:100=0,16
11%=11:100=0,11
Пусть масса первого раствора равна х мл,
тогда масса второго раствора равна (400-х) мл.
Масса соли в первом растворе равна 0,08х мл,
масса соли во втором растворе равна 0,16(400-х) мл.
По условию, получено 400 мл раствора концентрации 11%.
Составляем уравнение:
0,08х+0,16(400-х)=0,11*400
0,08х+64-0,16х=44
-0,08х = -20
х=-20:(-0,08)
х= 250 (мл) - масса первого раствора
400-250=150 (мл) - масса второго раствора
Если 8, то 24
Если 9, то 27
Если 10,то 30