по примеру реши.
x^3 - 6x^2 + 11x - 6 = 0 можно, конечно, решить формулой кардано для решения кубических уравнений, но это долго и трудно. проще подобрать корни схемой горнера. возможные рациональные корни x = a/b, где а - делитель свободного члена, b - делитель старшего коэффициента. x = 1, -1, 2, -2, 3, -3, 6, -6 находишь значения в этих точках. y(1) = 1 - 6 + 11 - 6 = 0 - повезло сразу! теперь раскладываем: x^3 - x^2 - 5x^2 + 5x + 6x - 6 = 0 (x - 1)(x^2 - 5x + 6) = 0 (x - 1)(x - 2)(x - 3) = 0 ответ: x1 = 1, x2 = 2, x3 = 3
1) 3ˣ < 1 + 12·3⁻ˣ|·3ˣ; (3ˣ)² < 3ˣ + 12; (3ˣ)² - 3ˣ - 12 < 0; (3ˣ)² - 3ˣ - 12 = 0; - квадратное уравнение относительно 3ˣ, отсюда 3ˣ = 4 или 3ˣ = -3 - не имеет решений.
Рисунок во вложении
ответ: (-∞; log₃4)
2) 4·4ˣ < 7·2ˣ + 2; 4·4ˣ - 7·2ˣ - 2 < 0; 4·(2ˣ)² - 7·2ˣ - 2 = 0 - квадратное уравнение относительно 2ˣ, отсюда D = 49 + 32 = 81; √D = 9; 2ˣ = (7 + 9)/8 = 2 или 2ˣ = (7 - 9)/8 = -1/4 - не имеет решений.
Рисунок во вложении
ответ: (-∞; 1).
3) 9ˣ - 6·3ˣ - 27 = 0; (3ˣ)² - 6·3ˣ - 27 = 0; - квадратное уравнение относительно 3ˣ отсюда 3ˣ = 9; x = 2 или 3ˣ = -3 - не имеет решений.
ответ: 2.
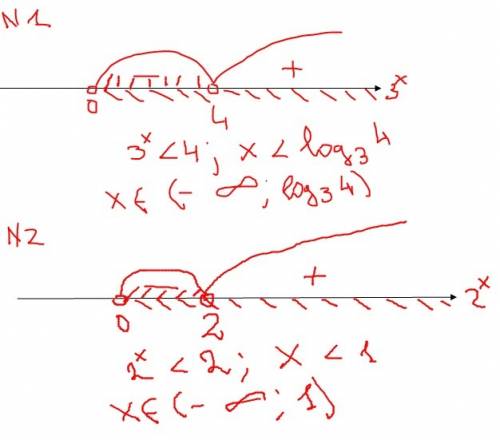
300
2. Требуемая сумма трёхсот членов этой арифметической прогрессии равна:
164850