1.
(x+7)(x-2)=x² - 2x+7x - 14=x²+5x-14
(y+5)(y²-3y+8)=y³-3y²+8y+5y²-15y+40=y³+2y² - 7y+40
(4c-d)(6c+3d)=24c²+12cd-6cd-3d²=24c²+6cd-3d²
2.
y(a-b)+2(a-b)=(a-b)(y+2)
3x-3y+ax-ay=3(x-y)+a(x-y)=(x-y)(3+a)
3.
xy(x+y)-(x²+y²)(x-2y)=x²y+xy² - (x³-2x²y+xy²-2y³)=x²y+xy²- x³+2x²y-xy²+2y³=2y³+3x²y - x³
4.
a(a-2)-8=(a+2)(a-4)
a²-2a-8=a²-2a-8
0=0 - верно
5.
х дм - ширина прямоугольника
х+12 (дм) - длина
х+12+3 (дм) - увеличенная длина
х+2 (дм) - увеличенная ширина
х(х+12)=(х+12+3)(х+2)-80
х²+12х=х²+17х+30-80
17х-12х=50
5х=50
х=10(дм) - ширина прямоугольника
10+12=22(дм) - длина
2x - y = -3; <=> y = 2x + 3. (1)
3x + y = -2; <=> y = -3x - 2. (2)
Построим графики функций (1) и (2). Координаты точки их пересечения и будут решением системы.
Функции (1) и (2) линейные, то есть их графиками являются прямые. Для построения прямой достаточно двух точек.
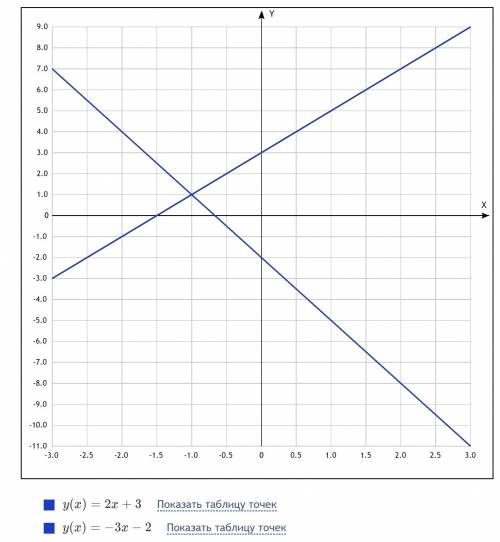
Строим график функции (1): при x = 0 y = 3; при x = 1 y = 5. Через точки (0, 3) и (1, 5) проводим прямую.
Строим график функции (2): при x = 0 y = -2; при x = -1 y = 1. Через точки (0, -2) и (-1, 1) проводим прямую.
По чертежу очевидно, что графики функций (1) и (2) пересекаются в точке (-1, 1). Следовательно, (-1, 1) - решение системы.
ответ: (-1, 1).
Чертеж:
(x^2 + 3x + 2) > x^2
3x + 2 > 0
x > -2/3