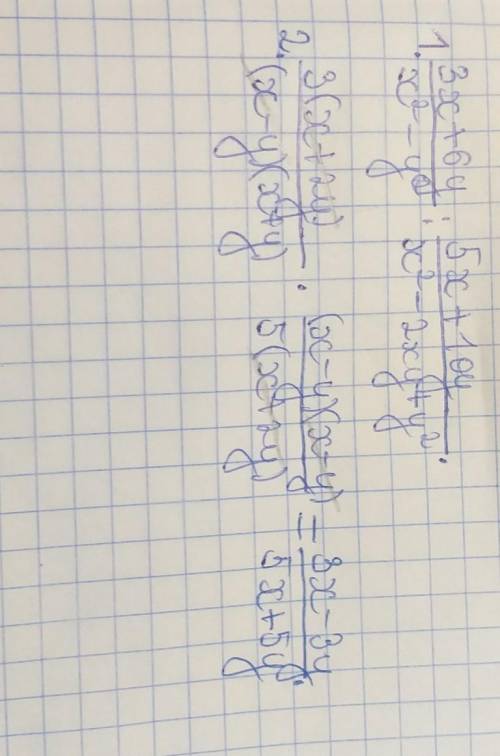x⁴=(3x-10)²
x⁴=9x²-60x+100
x⁴-9x²+60x-100=0
x₁=2
x⁴-9x²+60x-100 I_x-2
x⁴-2x³ I x³+2x²-5x+50
2x³-9x²
2x³-4x²
-5x²+60x
-5x²+10x
50x-100
50x-100
0
x³+2x²-5x+50=0
x₂=-5
x³+2x²-5x+50 I_ x+5
x³+5x² I x²-3x+10
-3x²-5x
-3x²-15x
10x+50
10x+50
0
x²-3x+10=0 D=-31 ⇒
Уравнение действительных корней не имеет.
ответ: х₁=2 х₂=-5.
Объяснение:
Удачи!!!
1. записываем пример.
2. раскрываем формулу разности квадратов (x^2-y^2) и закрываем формулу квадрата разности (x^2-2xy+y^2) и одновременно с этим проводим другие действия. при раскрытии формулы разности квадратов получается (x-y)(x+y). при закрытии формулы квадрата разности получается (x-y)^2. значит, это можно раскрыть как выражение (x-y), возведенное в квадрат, то есть, умножить это выражение на такое же. получается (x-y)(x-y). проводим остальные действия: выносим общие множители выражений за скобки и превращаем вторую дробь в обратную. в итоге получаются сократимые выражения, состоящие из множителей. (x+2y) сокращается в числителе первой дроби и в знаменателе второй. (x-y) сокращается в знаменателе первой дроби и в числителе второй. далее просто умножаем оставшиеся выражения на множители, которые выносили ранее. ответ:
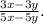
вывод. применение формул сокращенного умножения - их нужно закрывать или раскрывать в зависимости от того, что требуется в примере.