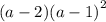
Алгоритм:
Как разложить уравнение высшей степени. По теореме Безу найти корень уравнения. Если найти корень не получается попробовать 1/2 и -1/2. Иначе подбирать (рекомендую ±1/3, ±2/3 и т.п.)
По схеме Горнера или уголком поделить уравнение на (x-a), где a - найденный в пункте 1 корень.
Продолжать до тех пор, пока в качестве одного из множителей не получится квадратное уравнение.
Применить алгоритм разложения на множители квадратного уравнения.
(как делать это быстро: подобрать корень, и подогнать под (x-a))
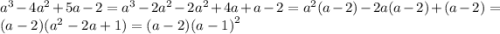
(см. объяснение)
Объяснение:
_________________________
(на самом деле нужно просто много таких пораскладывать и руку набить)
_________________________
Как разложить квадратное уравнение:
Найти дискриминант.Найти корни уравнения.Воспользоваться формулой: a(x-x1)(x-x2)Как разложить уравнение высшей степени:
По теореме Безу найти корень уравнения. Если найти корень не получается попробовать 1/2 и -1/2. Иначе подбирать (рекомендую ±1/3, ±2/3 и т.п.)По схеме Горнера или уголком поделить уравнение на (x-a), где a - найденный в пункте 1 корень.Продолжать до тех пор, пока в качестве одного из множителей не получится квадратное уравнение.Применить алгоритм разложения на множители квадратного уравнения.Теперь вернёмся к твоему уравнению:
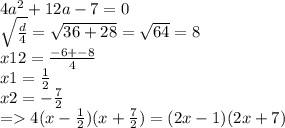
|c| = |a|*|b|*sin(a, b) = √(1^2+(-1)^2+0^2)*√(3^2+(-4)^2+0^2)*sin(pi/4) =
= √(1 + 1 + 0)*√(9 + 16 + 0)*1/√2 = √2*5*1/√2 = 5