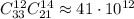
Xi 0 1/3 2/3 1
Pi 1/8 3/8 3/8 1/8
M[X]=1/2; D[X]=1/12; p=0,875.
Объяснение:
Частота появления события А является случайной величиной, обозначим её через X.
Так как грань с нечётным количеством очков может выпасть 0, 1, 2 или 3 раза, то частота появления принимает значения 0, 1/3, 2/3 и 1. При этом так как на игральной кости 3 грани с нечётным количеством очков и 3 - с чётным, то вероятность события А в одном опыте (то есть при одном бросании кости) равна 3/6=1/2. Найдём соответствующие вероятности:
P0=1/2*1/2*1/2=1/8; P1=3*1/2*1/2*1/2=3/8; P2=3*1/2*1/2*1/2=3/8; P3=1/2*1/2*1/2=1/8.
Проверка: p0+p1+p2+p3=1, так что вероятности найдены верно. Составляем закон распределения частоты появления события А:
Xi 0 1/3 2/3 1
Pi 1/8 3/8 3/8 1/8
Математическое ожидание M[X]=∑Xi*Pi=1/2; дисперсия D[X]=∑(Xi-M[X])²*Pi=1/12. Пусть событие А1 заключается в том, что событие A появится хотя бы в одном испытании. Для нахождения вероятности P(A1) рассмотрим противоположное ему событие B1, которое заключается в том, что грань с нечётным количеством очков не появится ни при одном броске. Так как события A1 и B1 - независимые и притом образуют полную группу, то P(A1)+P(B1)=1, откуда P(A1)=1-P(B1). А так как P(B1)=1/2*1/2*1/2=1/8, то P(A1)=1-1/8=7/8=0,875.
Свойства неравенств (нужные для решения задачи):
1. Обе части верного неравенства можно умножить на одно и тоже положительное число, при этом знак неравенства сохраняется.
2. Обе части верного неравенства можно умножить на одно и то же отрицательное число, при этом знак неравенства изменится на противоположный.
3. Неравенства одного знака можно складывать.
Поэтому:
a < 2, т.е. 5а < 10;
b > 3, т.е. -3b < -9,
тогда сложив полученные неравенства, получм неравенство
5а - 3b < 10 - 9, или 5а - 3b < 1.
Доказано.
Всего С(33;12)*С
Ввиду симметричности треугольника Паскаля варианты типа
С(33;12)*С(21;7)
С(33;14)*С(19;12)
С(33;7)*С(26;12)
И прочие будут давать тот же результат.