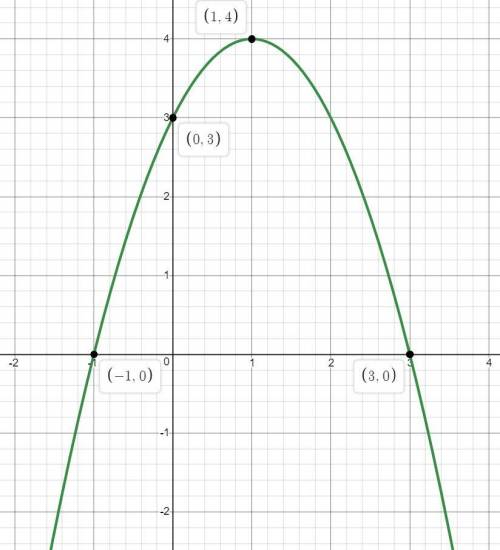
Построим график квадратной функции методом "по 3 точкам", а именно по вершине параболы и двум её корням (дискриминант не отрицательный).
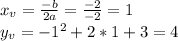
Это координаты вершины, почему именно такие? Корни уравнения:
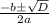, функция чётная (есть ось симметрии), и есть какая координата по оси Ох, которая меняется вправо и влево на одинаковое число.
Найдём нули функции:
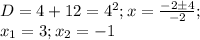
Суть в том, что мы отмечаем три точки на координатной плоскости и проводим ветви параболы, осознавая как именно растёт функции, функции x^2, то есть не надо ветви проводить как будто это уравнение прямой.
И чтоб всё было отмечено, найдём точки пересечения функции с осью Оу: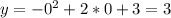 
то есть (0;3)
1) При x∈(-∞;-1)∪(3;+∞) функция принимает отрицательные значения
При x∈(-1;3) функция принимает положительные значения
2) При x∈(-∞;1) функция растёт
При x∈(1;+∞) функция убывает
3) Минимальное значение -∞, достигается в точках (-∞;-∞) или (+∞;-∞)
Максимальное значение 4, достигается в точке (1;4)
ответ: S=1,125 кв. ед.
Объяснение:
4.
y=x²-3x+4 y=4-x² S=?
x²-3x+4=4-x²
2x²-3x=0
x*(2x-3)=0
x₁=0 x=1,5
S=₀¹'⁵ (4-x₂-(x²-3x+4))dx=₀¹'⁵(3x-2x²)dx=(3/2)*x²-(2/3)*x³ ₀|¹'⁵=
=(3/2)*1,5²-(2/3)*1,5³=(3/2)*(1¹/₂)²-(2/3)*(1¹/₂)³=(3/2)*(3/2)²-(2/3)*(3/2)³=
=(3/2)³-(3/2)²=(3/2)²*(3/2-1)=(9/4)*(1/2)=9/8=1,125.
5.
В высшей точке скорость равна 0. ⇒
39,2-9,8*t=0
9,8*t=39,2 |÷9,8
t=4 (c).
v=39,2-9,8*t
s=₀∫⁴vdt=₀∫⁴(39,2-9,8*t)dt=39,2*t-9,8*t²/2 ₀|⁴=
=39,2*t-4,9*t² ₀|⁴=39,2*4-4,9*4²=156,8-78,4=78,4 (м).
ответ: наибольшая высота поднятия тела 78,4 м.