Пусть 
- канонический базис в 
.
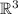Тогда матрицу перехода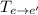 
можно найти следующим образом:
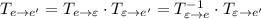
Если записать блочную матрицу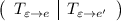 
и привести путем элементарных преобразований к виду 
, то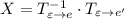 
Матрицу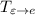 
легко получить: достаточно записать в столбцы координаты векторов базиса 
. Аналогично с матрицей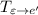 
.
В итоге необходимо получить вид следующей матрицы:
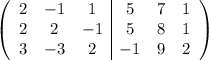
Вычтем первую строку из второй и третьей:
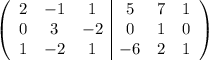
Вычтем из первой строки 2 третьих и поменяем их местами:
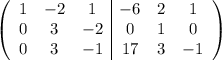
Вычтем из третьей строки вторую:
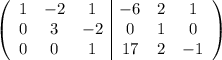
Прибавим ко второй строке 2 третьих и вычтем из первой третью:
Делим вторую строку на 3:
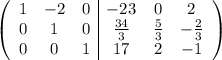
Прибавляем в первой строке 2 вторых:
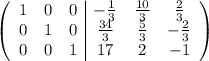
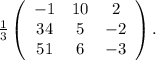
а
\begin{gathered} {x}^{2} + 4x + 10 \geqslant 0 \\ D = 16 + 40 < 0\end{gathered}x2+4x+10⩾0D=16+40<0
корней нет
Парабола выше оси ОХ, все у>0
2. Вся числовая прямая
б
\begin{gathered} {x}^{2} + 10x - 25 > 0 \\ D = 100 + 100 = 200 > 0\end{gathered}x2+10x−25>0D=100+100=200>0
2 корня, ветки параболы направлены вверх, у > 0 на 2 промежутках
6. Объединение двух промежутков
с
\begin{gathered} - {x}^{2} + 3x + 2 \leqslant 0 \\ {x}^{2} - 3x - 2 \geqslant 0 \\ D= 9 + 8 = 17 > 0\end{gathered}−x2+3x+2⩽0x2−3x−2⩾0D=9+8=17>0
2 корня, ветки параболы направлены вверх, у >=0 на двух промежутках
6. Объединение двух промежутков
d
\begin{gathered} - {x}^{2} - 4 > 0 \\ {x}^{2} + 4 < 0 \\ {x}^{2} + 4 = 0\end{gathered}−x2−4>0x2+4<0x2+4=0
корней нет, парабола выше ОХ, все у>0, отрицательных у нет
90км.ч=90000м/3600с =25м/с
25*15=375м длина поезда