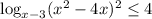
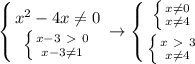 , следовательно,
, следовательно, 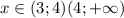
![\log_{x-3}(x^2-4x)^2\leq4;~\log_{x-3}(x^2-4x)^2-4\leq0;~\log_{x-3}(x^2-4x)^2-\\-\log_{x-3}(x-3)^4\leq0;~(x-3-1)[(x^2-4x)^2-(x-3)^4]\leq0;~\\(x-4)[(x^2-4x)^2-(x^2-6x+9)^2]\leq0;~\\(x-4)(x^2-4x-x^2+6x-9)(x^2-4x+x^2-6x+9)\leq0;~\\(x-4)(2x-9)(2x^2-10x+9)\leq0](/tpl/images/0775/5633/bf814.png)
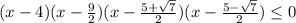
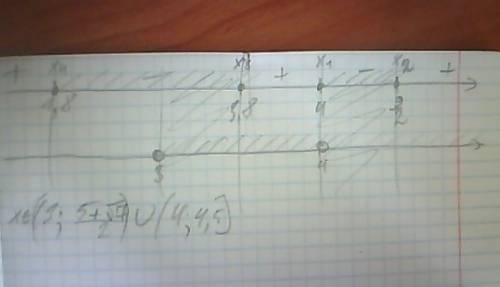
![x\in(3;\frac{5+\sqrt{7}}{2})(4;\frac{9}{2}]](/tpl/images/0775/5633/80e5d.png)
(2*X-3)*(2*X+3)-(4*X+5)*(X-3)=-1
ответ: 7+7*X=0
1) 4*X^2-9-(4*X+5)*(X-3)+1=0
1.1) (2*X-3)*(2*X+3)=4*X^2-9
(2*X-3)*(2*X+3)=2*X*2*X+2*X*3-3*2*X-3*3
1.1.1) 2*2=4
X2
_2_
4
1.1.2) X*X=X^2
X*X=X^(1+1)
1.1.2.1) 1+1=2
+1
_1_
2
1.1.3) 2*3=6
X2
_3_
6
1.1.4) 3*2=6
X3
_2_
6
1.1.5) 6*X-6*X=0
1.1.6) 3*3=9
X3
_3_
9
2) 4*X^2-9-(4*X^2-7*X-15)+1=0
2.1) (4*X+5)*(X-3)=4*X^2-7*X-15
(4*X+5)*(X-3)=4*X*X-4*X*3+5*X-5*3
2.1.1) X*X=X^2
X*X=X^(1+1)
2.1.1.1) 1+1=2
+1
_1_
2
2.1.2) 4*3=12
X4
_3_
12
2.1.3) -12*X+5*X=-7*X
2.1.4) 5*3=15
X5
_3_
15
3) 4*X^2-9-4*X^2+7*X+15+1=0
3.1) 4*X^2-9-(4*X^2-7*X-15)=4*X^2-9-4*X^2+7*X+15
4) -9+7*X+15+1=0
4.1) 4*X^2-4*X^2=0
5) 6+7*X+1=0
5.1) -9+15=6
-15
_ _9_
06
6) 7+7*X=0
6.1) 6+1=7
+6
_1_
7
Объяснение:
1)одинаковыми значками отмечены равные стороны. Значит
СО=ОД=4
Ао=ОВ=3
∠СОА=∠ВОД - вертикальные.
ΔСОА≅ΔДОВ по двум сторонам и углу между ними. значит и третьи стороны равны СА=ВД=5
5+4+3=12
ответ Р=12 см.
2)ΔАВС≅ΔСДА - по трем сторонам. СВ=ДА=6,АВ=СД=4,АС=7. Р=7+6+4=17 см.
ответ Р=17 см
3)АК=КВ=ВМ=МС ⇒АВ=ВС -суммы равных частей равны,значит треугольник АВС равнобедренный,а значит углы при основании равны! ∠А=∠С
ΔАКД≅ΔСМД по двум сторонам и углу между ними(АК=МС,∠А=∠С,АД=ДС) ⇒КД=МД -против равных углов в равных треугольниках лежат равные стороны
КВ=ВМ -дано,ВД -общая.(равна сама себе) . Отсюда по трем сторонам ΔКВД≅ΔМВД что и требовалось доказать.
4)АК=КВ=ВМ=МС ⇒АВ=ВС -суммы равных частей равны,значит треугольник АВС равнобедренный,а значит углы при основании равны! ∠А=∠С
ΔАКД≅ΔСМД по двум сторонам и углу между ними(АК=МС,∠А=∠С,АД=ДС)
{x-3>0⇒x>3
{x-3≠1⇒x≠4
{x²-4x≠0⇒x(x-4)≠0⇒x≠0 U x≠4
x∈(3;4) U (4;∈(3;4)
(x²-4x)²≥(x-3)^4
(x²-4x)²-(x-3)^4≥0
(x²-4x)²-(x²-6x+9)²≥0
(x²-4x-x²+6x-9)(x²-4x+x²-6x+9)≥0
(2x-9)(2x²-10x+9)≥0
2x-9=0⇒x=4,5
2x²-10x+9=0
D=100-72=28
x1=(10-2√7)/4=2,5-0,5√7 U x2=2,5+0,5√7
_ + _ +
[2,5+0,5√7](3)[2,5+0,5√7](4)[4,5]
x∈(3;2,5+0,5√7]
2)x∈(4;∞)
_ + _ +
[2,5+0,5√7](3)[2,5+0,5√7](4)[4,5]
x∈(4;4,5]
ответ x∈(3;2,5+0,5√7] U (4;4,5]