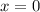 .
.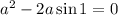 . Выносим общий множитель, получим
. Выносим общий множитель, получим 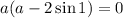 откуда
откуда 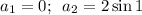
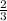 от того, что осталось после первого деня, то после второго дня работы осталась
от того, что осталось после первого деня, то после второго дня работы осталась  от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно
от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно  =2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
=2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
Пусть a = 0.
Тогда
Графиком первой функции является парабола. Вторая функция будет являться чётной:
y(-x) = 2sin(cos(-x) = 2sincosx, значит, y(x) = y(-x).
Найдём область значений второй функции:
Пусть y = f(x) = 2sin(g(x))
E(g) = [-1; 1]
Тогда E(x) = [2sin(-1); 2sin1]
Чтобы парабола и данная периодическая функция пересекались в одной точке, вершина параболы должна лежать на графике периодической функции. Это будет только тогда, когда значение a будет равно наибольшему значению из области значений периодической функции, т.е. a = 2sin1.
ответ: при a = 2sin1; 0.