На протяжении всей истории математики[⇨] представление о и допустимых методах доказательства существенно менялось, в основном, в сторону большей формализации и бо́льших ограничений. Ключевой вехой в вопросе формализации доказательства стало создание математической логики[⇨] в XIX веке и формализация её средствами основных техник доказательства. В XX веке построена теория доказательств — теория, изучающая доказательство как математический объект[⇨]. С появлением во второй половине XX века компьютеров особое значение получило применение методов математического доказательства для проверки и синтеза программ[⇨], и даже было установлено структурное соответствие между компьютерными программами и математическими доказательствами (соответствие Карри — Ховарда[⇨]), на основе которого созданы средства автоматического доказательства[⇨].
Объяснение:
Основные приёмы, используемые при построении доказательств: прямое доказательство[⇨], математическая индукция и её обобщения[⇨], доказательство от противного[⇨], контрапозиция[⇨], построение[⇨], перебор[⇨], установление биекции[⇨], двойной счёт[⇨]; в приложениях в качестве математических доказательств привлекаются также методы, не дающие формального доказательства, но обеспечивающие практическую применимость результата[⇨] — вероятностные, статистические, приближённые. В зависимости от раздела математики, используемого формализма или математической школы не все методы могут приниматься безоговорочно, в частности, конструктивное доказательство[⇨] предполагает серьёзные ограничения.
ну смотри.
Возьмём в пример это:
(а+4)(6+а)
Мы должны умножать дугой: а×6=6а, а×а=а², 4×6=24, 4×а=4а.
Я прикреплю фото, чтобы было понятнее.
ответом будет являться: 6а+а²+24+4а.
Но ответ не окончательный, убираем подобные: 6а и 4а.
ответ: 10а+а²+24.
Выражение в виде произведения многочленов.
Пример:
а(m-3)+b(m-3)
В данном случае общим множителем является многочлен m-3. Поэтому выносим его в начало, а множители за скобками складываем и умножаем;
(m-3)(a+b)
Метод группировки.
Метод группировки - это разложение многочлена на множители, объединив в группы его члены.
Пример:
2ас+2bc+5am+5bm
Сгруппировать члены этого многочлена нужно так, чтобы слагаемые в каждой группе имели общий множитель.
2ас+2bc+5am+5bm=(2ac+2bc)+(5am+5bm)=
=2c(a+b)+5m(a+b)=(a+b)(2c+5m).
Ничего сложного нет, нужно это только понять.)
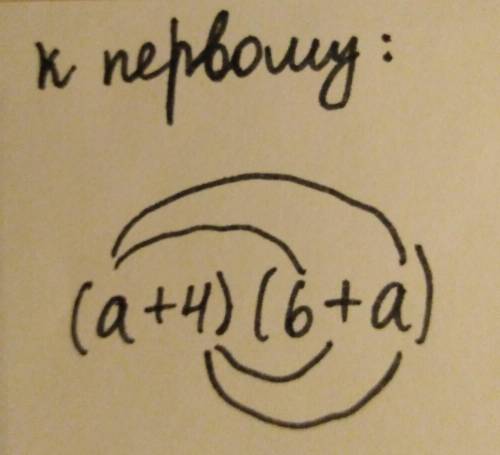
масса меди в 10 кг 40% сплава:
m₁ = 10*0,4 = 4 (кг)
масса меди в х кг 10% сплава:
m₂ = 0,1x (кг)
масса меди в х+10 кг 30% сплава:
m₁₂ = 4 + 0,1x (кг)
так как в х+10 кг конечного сплава содержится:
m₁₂ = 0,3*(х+10) кг меди, то:
4 + 0,1x = 0,3*(x+10)
4 - 3 = 0,2x
x = 5 (кг)
Проверим: 10*0,4 + 5*0,1 = 0,3*(5 + 10)
4 + 0,5 = 0,3 * 15
4,5 = 4,5 (масса меди в 15 кг 30% сплава)
ответ: 5 кг.