y = 4x - x² - Квадратичная функция, график - парабола, ветви направлены вниз ( a = -1). Максимальное значение принимает в вершине, минимальное значение не имеет, снизу не ограничена.
a) Координаты вершины параболы
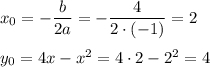
x₀=2 ∈ [0; 3] ⇒ x₀=2 - точка максимума функции попадает в заданный интервал, наибольшее значение функции y₀ = 4.
Значения функции на границах интервала
x = 0; y = 4·0 - 0² = 0
x = 3; y = 4·3 - 3² = 3
Наименьшее значение y = 0 при x = 0.
б) x∈(-∞; 2] - функция возрастает
x∈[2; +∞) - функция убывает
в) 4x - x² < 0 ⇔ x (4 - x) < 0
Метод интервалов : x₁ = 0; x₂ = 4
------------ (0) +++++++++ (4) -----------> x
x∈(-∞; 0) ∪ (4; +∞)
1 C
2 A
3. 40√6
4 √14 , 3√2, 23
5. 2√11
6. пройдет
Объяснение:
2. Возведем в квадрат √ и границы интервалов и увидим
3. √96100 = √(6*16*100) = 40√6
4. возведем в квадрат: 14, 529, 18
5. 22/√11 = 2√11√11 / √11 = 2√11
6. так же возведем в квадрат H² = 32, h² = 29.16 h<H пройдет
7. = 3* (3-√b- 3 -√b) / (9-b) - 2b/ (9-b) = (6√b+2b)/b-9 = 2√b(3+√b)/(9-b)
непонятно зачем там про а сказано...
8. а) √а = 8√3
√а = √192
а = 192
b) √0 = 0, √36 = 6
у ∈ [0;6]
c) 14² = 196
28² = 784
x ∈ [196; 784]
d) y≤5
√x≤5
x ≥0
x≤ 25
x ∈ [0;25]
Объяснение:
(√a)²=a
√(a)²=IaI
√48=√16*3=4√3
√18-√32+√8= √2*9-√16*2+√4*2= 3√2-4√2+2√2=5√2-4√2=√2
(V²+2√3)(2√3-√2)=(2√3+√2)(2√3-√2)=4*3-2=12-2=10