1) a)y=3 б)x=3 в) (3;+∞) возрастает (-∞;3) убывает
2)а)у=-0,5 б) у=0,25 в) у=3
3) у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)
Объяснение:
1) находим по графику абсцисса -это х ордината это -у
2)подставляем вместо х значение и считаем
3) a)у(4)=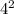 =16 б)у(-3)=
=16 б)у(-3)=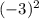 =9 в) у(2)=
=9 в) у(2)=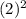 =4
=4
у(3)=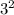 =9 у(-2)=
=9 у(-2)=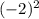 =4 у(-5)=
=4 у(-5)=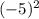 =25
=25
у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)
(х + 6) * (х - 3)
Объяснение:
Розв'яжемо цей квадратний тричлен як квадратне рівняння:
х^2 + 3х - 18 = 0
За теоремою Вієта:
х1 + х2 = -3
х1 * х2 = -18
Підбираємо такі значення х1 і х2, щоб вони відповідали цій системі рівнянь. Це (-6) і 3.
Скористаємось формулою розкладання квадратного тричлена на множники, а саме:
ах^2 + bx + c = a * (x - x1) * (x - x2)
Виходячи з того, ща в нашому рівнянні а=1, х1 = -6, х2 = 3, підставимо ці значення в формулу:
a * (x - x1) * (x - x2) = 1*(х - (-6)) * (х - 3) = (х + 6) * (х - 3)
Маємо квадратний тричлен, розкладений на множники
m+n=0.5n m=-0.5*n→m>0 не может
m+n=mn→m=0→не может
не может
m+n=-n m=-2n n<0→m>0 не может
m+n=m n=0 не может