- сумма кубов
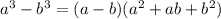-разность кубов
- разность квадратов
З'ясуємо, як знайти область визначення деяких функцій, заданих формулою.
1. Якщо функція — многочлен, то вона існує при будь-яких значеннях аргумента, тобто її область визначення — всі дійсні числа.
2. Якщо функція задана формулою, яка містить аргумент у знаменнику дробу, то до області визначення функції входять всі дійсні числа, крім тих, які перетворюють знаменник в нуль.
3. Якщо функція задана формулою, яка містить арифметичний квадратний корінь, то до області її визначення входять всі дійсні числа, при яких підкореневий вираз набуває невід'ємних значень.
Область значень функції (множина значень) - усі значення, яких набуває функція.
Функція є парною - якщо для будь-якого х з області визначення функції виконується рівність f(x)=f(-x)
Функція є непарною - якщо для будь-якого х з області визначення функції виконується рівність f(-x)=-f(x)
Объяснение:
2(6-2x)(7-3x)-12(2x-1²)>4(2-3x)(3x+2)-8(2x-7) |2
42-18x-14x+6x²-12x+6>2(4-9x²)-8x+28
6x²-44x+48>8-18x²-8x+28 |2
3x²-22x+24>-9x²-4x+18
3x²+9x²-18x+6>0
12x²-18x+6>0 |6
2x²-3x+1>0
Допустим 2x²-3x+1=0
2x²-x-2x+1=0
(2x²-2x)-(x-1)=0
2x(x-1)-(x-1)=0
(2x-1)(x-1)=0
2x-1=0; 2x=1; x₁=1/2=0,5
x-1=0; x₂=1
Для определения знака функции возьмём пробную точку на интервале (-∞; 0,5), например, 0:
2·0²-3·0+1=0-0+1=1; 1>0
+ - +
°°>x
0,5 1
ответ: x∈(-∞; 0,5)∪(1; +∞).
P¹²-1=(р⁴-1)(р⁸-р⁴+1)=(р²+1)(р²-1)(р⁸-р⁴+1)=(р+1)(р-1)(р²+1)(р⁸-р⁴+1)