 и
и 
Объяснение:
Первый модуль обращается в ноль при x=-2, второй - при 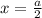 .
.
Пусть сначала
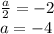
Тогда уравнение принимает вид  и, очевидно, не имеет решений.
и, очевидно, не имеет решений.
Пусть теперь
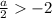
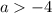
Если  , то оба модуля раскрываются с плюсом и уравнение принимает вид:
, то оба модуля раскрываются с плюсом и уравнение принимает вид:
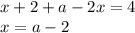
Полученный x будет корнем уравнения, если он принадлежит рассматриваемому отрезку, то есть если  удовлетворяет системе неравенств
удовлетворяет системе неравенств

Решение системы: 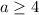
Если 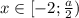 , то уравнение принимает вид
, то уравнение принимает вид
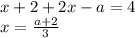
Полученный x будет корнем уравнения, если  удовлетворяет системе:
удовлетворяет системе:

Решение системы: 
Пусть, наконец, 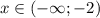 . Тогда уравнение принимает вид
. Тогда уравнение принимает вид
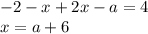
Полученный x будет корнем уравнения, если  удовлетворяет системе:
удовлетворяет системе:
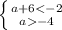
Эта система не имеет решений.
Теперь пусть  , то есть
, то есть 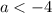 .
.
Если  , то
, то
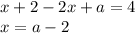
Система:
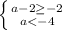
Нет решений.
Если  , то
, то
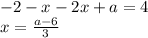
Система:
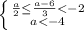
Решение системы: 
И наконец, если 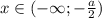 , то
, то
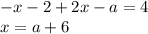
Система:
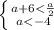
Решение: 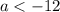
Из вышесказанного очевидно, что
При  - два решения
- два решения
При  - одно решение
- одно решение
При  - нет решений
- нет решений
При  - нет решений
- нет решений
При  - одно решение
- одно решение
При  - два решения
- два решения
Таким образом, уравнение имеет одно решение при  и
и 
 и
и 
Объяснение:
Первый модуль обращается в ноль при x=-2, второй - при 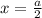 .
.
Пусть сначала
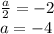
Тогда уравнение принимает вид  и, очевидно, не имеет решений.
и, очевидно, не имеет решений.
Пусть теперь
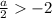
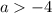
Если  , то оба модуля раскрываются с плюсом и уравнение принимает вид:
, то оба модуля раскрываются с плюсом и уравнение принимает вид:
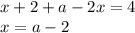
Полученный x будет корнем уравнения, если он принадлежит рассматриваемому отрезку, то есть если  удовлетворяет системе неравенств
удовлетворяет системе неравенств

Решение системы: 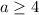
Если 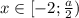 , то уравнение принимает вид
, то уравнение принимает вид
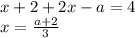
Полученный x будет корнем уравнения, если  удовлетворяет системе:
удовлетворяет системе:

Решение системы: 
Пусть, наконец, 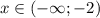 . Тогда уравнение принимает вид
. Тогда уравнение принимает вид
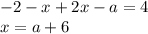
Полученный x будет корнем уравнения, если  удовлетворяет системе:
удовлетворяет системе:
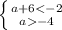
Эта система не имеет решений.
Теперь пусть  , то есть
, то есть 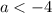 .
.
Если  , то
, то
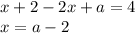
Система:
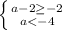
Нет решений.
Если  , то
, то
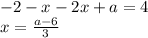
Система:
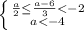
Решение системы: 
И наконец, если 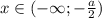 , то
, то
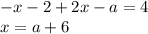
Система:
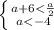
Решение: 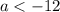
Из вышесказанного очевидно, что
При  - два решения
- два решения
При  - одно решение
- одно решение
При  - нет решений
- нет решений
При  - нет решений
- нет решений
При  - одно решение
- одно решение
При  - два решения
- два решения
Таким образом, уравнение имеет одно решение при  и
и 
Здесь: a - коэффициент перед x²
b - коэффициент перед x
c - свободный член
Это стоит один раз запомнить, а потом всегда пользоваться.
Кстати, дискриминант в этих формулах тоже есть, он равен:
1.
Здесь: a = 3; b = -1; c = 1;
Подставляем:
Под корнем отрицательное число (дискриминант меньше нуля), следовательно, действительных решений нет.
2.
Здесь: a = -6; b = 37; c = -6;
Подставляем:
3.
Здесь: a = 9; b = 24; c = 16
Подставляем:
А вот и третий случай, когда дискриминант равен нулю (это то, что под корнем). В этом случае второй корень равен первому.