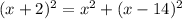
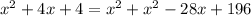
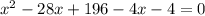
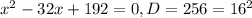
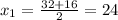
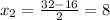
Займусь своим любимым делом - упрощением уравнения. Но сначала выпишем ОДЗ: ![x\in[0;1] -](/tpl/images/0329/6763/5c625.png)
это очевидное следствие наличия двух радикалов. Далее: обращаю внимание на то, что в двух случаях "x" входит в уравнение с коэффициентом 5. А ведь скорее всего придется в квадрат возводить... В общем, домножаю уравнение на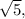 
занося сразу этот множитель под знаки радикалов:
![(5x+2)\cdot\sqrt{5-5x}+(5x-7)\cdot\sqrt{5x}=0; 5x=t\in[0;5];](/tpl/images/0329/6763/65e51.png)
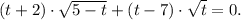
На мой взгляд, уравнение стало выглядеть чуть привлекательней. Но это не предел. В уравнение неизвестная входит четыре раза. Надо бы уменьшить. Проверяем подстановкой, является ли решением t=0 - не является. Поэтому можно поделить уравнение на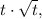 
записав теперь его в виде
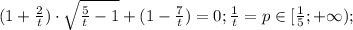
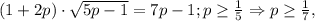
то есть это уравнение можно смело возводить в квадрат без боязни приобрести лишние корни:
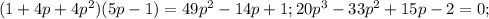
угадываем p=1; делим столбиком или угадываем разложение любым другим доступным ниже нашего достоинства говорить о таких мелочах, когда решаешь такую продвинутую задачу):
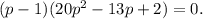
Итак, одно решение у нас уже есть (надо только не забыть в конце вернуться к первоначальной переменной), остается решить квадратное уравнение. Желающие могут вычислять дискриминант, мы же продолжим идти путем упрощенчества. Домножим уравнение
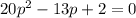на 20 и сделаем замену (последнюю!) 20p=q:
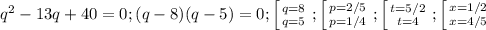
Дополнительно было решение p=1; t=1; x=1/5.
ответ: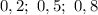 
значит так
Объяснение:
-1.4*6=-8.4
-5.6:(-7)=0.8
0.6:(-1.2)=-0.5
2.5*0.04=0.1
-6.03+0.63=-5.4
0.37-5.63=-5.26
-5.6:100=-0.056
-0.001*(-63)=0.063
11:0.01=1.1
2*(-2.077)*5=-20.77