Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
y = (x² - x - 20)² - 18
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
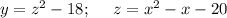
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
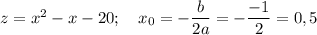 - координата вершины
- координата вершины
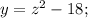 z = 0 - координата вершины параболы
z = 0 - координата вершины параболы

x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
2.Из условия x0=-a=2, отсюда a=-2, y=x^2-4x+3, подставляем (3;0), получаем 0=9-12+3=0 значит ответ да
3. Ну по идее нужно обнулить икс, поэтому 2x-1>0, x-1<0, x-2<0, получаем
x>1/2, x<1, x<2, то есть если a=2 у нас все числа от 1/2 до 1 являются корнями. ответ да
4.Рассмотрим x^3-ax-1=0. x=0 не является корнем ни при каком a, значит это уравнение равносильно исходному. Если у кубического многочлена 2 действительных корня, то обязательно один из них кратный (потому что комлексных корней у многочлена четное количество), отсюда x^3-ax-1=(x-p)^2(x-t). Раскрываем скобки приравниваем соответствующие коэффициенты друг другу получаем что