Приклад:
Розв'язати систему рівнянь: {x−2y=3,5x+y=4.
1) З першого рівняння системи виражаємо змінну x через змінну y.
Отримуємо: x−2y=3,x=3+2y;
2) Підставимо отриманий вираз замість змінної x у друге рівняння системи:
5⋅x+y=4,5⋅(3+2y)+y=4;
3) Розв'яжемо утворене рівняння з однією змінною, знайдемо y:
5⋅(3+2y)+y=4,15+10y+y=4,10y+y=4−15,11y=−11,|:11y=−1¯¯¯¯¯¯¯¯¯¯¯.
4) Знайдемо відповідне значення змінної x, підставивши значення змінної y, у вираз знайдений на першому кроці:
x=3+2⋅y,x=3+2⋅(−1),x=3−2,x=1¯¯¯¯¯¯¯¯.
5) Відповідь: (1;−1) .
Объяснение:
это решить линейные уравнения без черчежей
Алгоритм решения системы двух уравнений с двумя переменными методом подстановки:
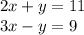
1. из любого (обычно более простого) уравнения системы выразить одно неизвестное через другое,например, у через х из первого уравнения системы;
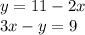
2. подставить полученное выражение в другое (второе) уравнение системы вместо у;
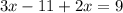
3. решить уравнение с одним неизвестным относительно х (найти х);
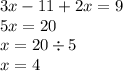
4. подставить найденное на третьем шаге значение х в уравнение,полученное на первом шаге, вместо х и найти у;
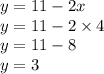
5. записать ответ.
ответ: х=4, у=3.
30x-20-15x-6+55-20x=25
-5x+29=25
-5x=-4
x=0.8