Обозначим за х время. за которое Вася с утра шёл от дома до школы
1) х - время, за которое Вася от дома до школы
2) в (8+х) часов он был в школе
3) в (8+х+5) часов , то есть в (13+х) часов у Васи закончились уроки, он вышел из школы и пошёл домой
4) до дома Вася шёл в 3 раза дольше, чем до школы. До школы он дошёл за х часов, значит, до дома за 3х часов
5) итак, Вася вышел из школы в (13+х) часов (см пункт 3) и дошёл до до дома за 3х часов (см пункт 4)
Получается в (13+х+3х) часов (то есть в (13+4х) часов) Вася был дома
6) А по условию задачи Вася был дома в 15 часов
Значит, 13+4х=15
7) решаем это уравнение:
13+4х=15
4х=15-13
4х=2
х=1/2 (ч)
7) то есть с утра Вася шёл от дома до школы 0,5 часа (это я только что выяснил в пункте 7) со скоростью 4 км/час (по условию задачи)
Расстояние= скорость*время= 4 км/час* 0,5 ч= 2 км
ответ: Школа находится в 2 км от дома
Сторона данного треугольника а(3) равна Р:3=6√3:3=2√3 дм
Формула радиуса окружности, описанной около правильного треугольника:
R=a/√3 =>
R=2√3:√3=2 дм
Формула стороны правильного многоугольника через радиус вписанной окружности:
а(n)=2r•tg(180°:n), где r – радиус вписанной окружности, n – число сторон,
Для правильного шестиугольника tg(180°:n)=tg30°=1/√3
a₆=2•2•1/√3=4/√3
P=6•4/√3=8√3 дм
—————
Как вариант: Правильный шестиугольник состоит из 6 равных правильных треугольников.
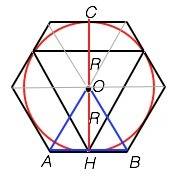
На рисунке приложения ОН - радиус описанной около правильного треугольника окружности и в то же время высота одного из 6 правильных треугольников, все углы которого 60°; АВ - сторона шестиугольника. Задача решается с т.Пифагора.