Объяснение:
1) Положим, существует такое число, которое может выразиться несократимой дробью 
, при этом p - целое, q - натуральное, которое удовлетворяет соотношению:
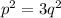
Из этого следует, что p², и p делятся на 3. Тогда p можно представить как 3c, тогда уравнение перепишется в виде:
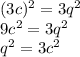
Отсюда следует, что и q делится на 3, а это противоречит условию несократимости дроби изначально. Следовательно на множестве рациональных чисел решений нет.
2) UPD: решается так же, немного не тот путь указал.
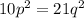
p² и p делятся на 21, значит p представимо в виде p = 21c
Тогда:
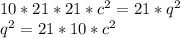
Стало быть, q тоже делится на 21, условие о несократимости дроби p/q нарушена, и значит решений нет на рациональном множестве
Пусть х км/ч - скорость течения реки, тогда (18 + х) км/ч - скорость катера, идущего по течению реки, (16 - х) км/ч - скорость катера, идущего против течения реки. Катер, идущий по течению до встречи (18 + х) · 1,5 км, а катер, идущий против течения до встречи (16 - х) · 0,5 км. Так как по условию задачи расстояние между пристанями 37 км и катера встретились, то вместе они расстояние (18 + х) · 1,5 + (16 - х) · 0,5 км, что составляет 37 км. Решим уравнение:
(18 + х) · 1,5 + (16 - х) · 0,5 = 37
27 + 1,5х + 8 - 0,5х = 37
1,5х - 0,5х = 37 - 27 - 8
х = 2
ответ: 2 км/ч.
X(x-1)>0;
x>0
x>1
+ - +
-oo01+oo
Xє(-оо;0)U(1;+00);
2)x^2-4>0
X^2>4
X1,2>+/-2
+ - +
-oo-22+oo
Xє(-оо;-2)U(2;+oo);
3)a^2>225
A1,2>+/-15
Аналогично:
xє(-оо;-15)U(15;+oo);
4)(x+2)(x+4)(x-1)>0
X>-2;
X>-4
X>1
- + - +
-oo-4-21+oo
Xє(-4;-2)U(1;+oo)