• приравниваем (x^2-1)(x+2) к нулю.
• расписываем скобку (х^2-1) по формуле разности квадратов: (х-1)(х+1)
• решаем уравнение относительно х: (х-1)(х+1)(х+2)=0
х-1=0 или х+1=0 или х+2=0
х=1 х=-1 х= -2
• на координатной прямой отмечаем полученные корни: -2; -1; 1
• точки выколотые, так как знак неравенства строгий
• из промежутка от - бесконечность до -2 выбираем любое число, например, -3. Подставляем его в выражение (х^2-1)(х+2): (9-1)(-3+2)= -1*8= -8. Произведение отрицательное, значит на этом промежутке отрицательные значения. Ставим минус.
• так же делаем с каждым промежутком
• ищем промежутки, на которых выражение (х^2-1)(х+2) >0 ( т.е промежутки с «+» )
ответ: х принадлежит (-2;-1) u (1; + бесконечность)
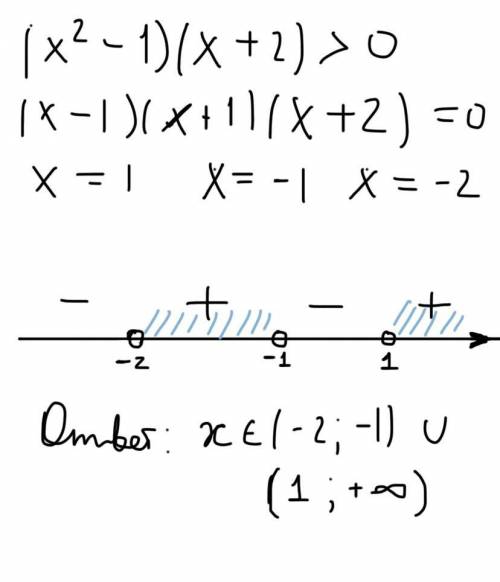
Объяснение:
1) 2 в степени 1/3 И 2 в степени 2/3 - основания > 1 и равны 2, значит, сравнивает степени (1/3) < (2/3) Зависимость прямая : чем больше степень, тем больше число.
2 в степени 1/3 < 2 в степени 2/3
2) (2) в степени 1/4 И (2)в степени 3/4 - основания > 1 и равны 2, значит, сравниваем степени : (1/4) < (3/4) Зависимость прямая : чем больше степень, тем больше число.
(2) в степени 1/4 < (2)в степени 3/4
3) (1/3) в степени 2 И (1/3) в степени 3 - основания < 1 и равны 1/3, значит, сравниваем степени : (1/4) < (3/4) - Зависимость обратная : чем больше степень, тем меньше число.
(1/3) в степени 2 > (1/3) в степени 3/4
Выбор зависимости зависит от основания. Если основание >1, то зависимость прямая. Если основание 0<..<1, то зависимость обратная
350 кг - 100%
0.021 кг - ?
0.021* 100% : 350 = 0.006 %
значит, в растворе содержится 0.006% соли