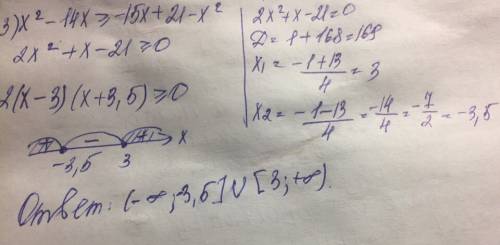
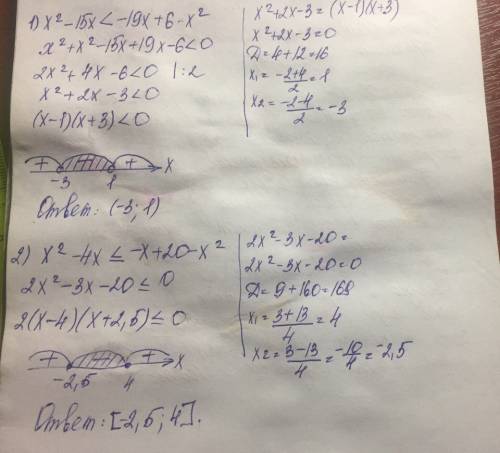
1) 11х = 36 - х
ОДЗ уравнения:
x ∈ ( -∞, ∞)
Делаем преобразование правой части уравнения:
36 - x = - ( x - 36)
Уравнение после преобразования:
11x = - (x - 36)
Упрощаем:
12x = 36
Сокращаем:
12(убираем)x = 12(убираем) * 3
x=3
2) 9х + 4 = 48 - 2х
ОДЗ уравнения:
x ∈ ( -∞, ∞)
Делаем преобразование правой части уравнения:
48 - 2x = -2 * (x - 24)
Уравнение после преобразования:
9x + 4 = -2 * (x - 24)
Упрощаем:
11x = 44
Сокращаем:
11(убираем)x = 11(убираем) * 4
x=4
3) 8 - 4х = 2х - 16
ОДЗ уравнения:
x ∈ ( -∞, ∞)
Делаем преобразование левой части уравнения:
8 - 4x = -4 * (x - 2)
Делаем преобразование правой части уравнения:
2x - 16 = 2 * (x - 8)
Уравнение после преобразования:
-4 * (x - 2) = 2 * (x - 8)
Упрощаем:
-6x = -24
Сокращаем:
-6(убираем)x = -6(убираем) * 4
x = 4
За остальным, если желаешь - в ЛС.
Первую ещё не придумала, а вот вторая:
Чтобы найти вероятность того, что точка,брошенная в круг, попадёт в треугольник, надо найти отношение площади правильного треугольника к площади окружности
S(треуг)=(а:2*корень(3))/ S 4
S(окруж)=Pі *r^2
Мы знаем связь между стороной правильного треугольника и радиусом описаной окружности:
r=a/корень3
Тогда, вероятность = S(треуг)/ S(окруж)= ((а:2*корень(3))/ S 4) / (Pі *r^2) = ((а:2*корень(3))/ S 4) * (Pі *а^2) /3=(3*корень3)/ 4Pі
Если надо, можно примерно вищитать:
(3*корень3)/ 4Pі = 3*1,73/4*3,14=5,19/12,56=0,41
ответ:0,41
2x² + 4x - 6 < 0 |:2
x² + 2x - 3 < 0
x² + 2x + 1 - 4 < 0
(x + 1)² - 2² < 0
(x + 1 - 2)(x + 1 + 2) < 0
(x - 1)(x + 3) < 0
Нули: x = -3; 1.
00> x
+ -3 - 1 +
ответ: x ∈ (-3; 1).
2. x² - 4x ≤ -x + 20 - x²
2x² - 3x - 20 ≤ 0
2x² - 8x + 5x - 20 ≤ 0
2x(x - 4) + 5(x - 4) ≤ 0
(2x + 5)(x - 4) ≤ 0
Нули: x = -2,5; 4.
●●> x
+ -2,5 - 4 +
ответ: x ∈ [-2,5; 4]
3) x² - 14x ≥ -15x + 21 - x²
2x² + x - 21 ≥ 0
2x² - 6x + 7x - 21 ≥ 0
2x(x - 3) + 7(x - 3) ≥ 0
(2x + 7)(x - 3) ≥ 0
Нули: x = -3,5; 3.
●●> x
+ -3,5 - 3 +
ответ: x ∈ (-∞; -3,5] U [3; +∞).