Объяснение:
Мы докажем это равенство по индукции. Но сначала преобразуем правую часть равенства к более удобному для нас виду:
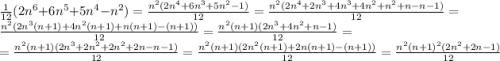А вот теперь применим индукцию. Легко проверить, что для n=1 равенство верно.
Теперь предположим что равенство верно для n=k:
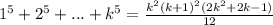
Прибавив к обеим частям равенства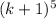 
получим:
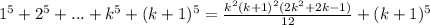
Займёмся преобразованием правой части этого равенства:
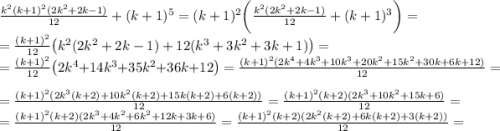
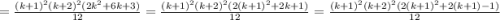Таким образом
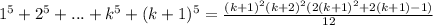
То есть если равенство верно для произвольного n=k, то оно также оказывается верным и для n=k+1. По индукции заключаем верность равенства для любого натурального n.
Если же вас интересует каким можно вывести формулу, которую мы только что доказали - напишите мне в ЛС.
Приклад:
Розв'язати систему рівнянь: {x−2y=3,5x+y=4.
1) З першого рівняння системи виражаємо змінну x через змінну y.
Отримуємо: x−2y=3,x=3+2y;
2) Підставимо отриманий вираз замість змінної x у друге рівняння системи:
5⋅x+y=4,5⋅(3+2y)+y=4;
3) Розв'яжемо утворене рівняння з однією змінною, знайдемо y:
5⋅(3+2y)+y=4,15+10y+y=4,10y+y=4−15,11y=−11,|:11y=−1¯¯¯¯¯¯¯¯¯¯¯.
4) Знайдемо відповідне значення змінної x, підставивши значення змінної y, у вираз знайдений на першому кроці:
x=3+2⋅y,x=3+2⋅(−1),x=3−2,x=1¯¯¯¯¯¯¯¯.
5) Відповідь: (1;−1) .
Объяснение:
это решить линейные уравнения без черчежей
3*(-1,4) + 4*3,7 = -4,2 + 14,8 = 10,6