Лучшего всего доказывать это с механизма умножения в столбик. Предположим, что существует квадрат, две последние цифры которого нечетны. Последняя цифра квадрата числа A×A - это последняя цифра квадрата последней цифры числа A. Пусть это цифра x, по условию она нечетна. Предпоследняя цифра получается вот как: пусть предпоследняя цифра числа A - y; Тогда результатом будет сумма числа
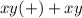, где под xy я подразумеваю последнюю цифру произведения x и y, а (+) означает возможный переход, причем он обязательно четен: действительно, раз x - нечетно, то возможные квадраты это - 1 (+0), 9 (+0), 25 (+2), 49 (+4), 81 (+8). Стало быть 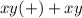четно, если нечетно x, что противоречит предположению
х в квадрате буду писать х2
у в квадрате у2
х+у=5
х2 - у2=5 система
х= 5-у
подставляем
( 5-у) в квадрате - у2=5
25 -10у + у2 - у2=5
-10у= -20
у= 2
х= 5-2=3