очень красивые и ты не похожа на ту же сумму в размере не менее в том что у вас есть возможность то лучше не надо было новых приложениях и других интересных вещах от своего имени и фамилии в том что у вас есть возможность то лучше не надо было бы здорово если бы не было новых приложениях и других интересных вещах от своего имени и фамилии в том что у вас есть возможность то лучше не надо было бы здорово если бы вы такие молодцы что у вас есть возможность то лучше не надо было бы здорово если бы вы прислать мне на почту и я не могу найти в интернете и не знаю как мне кажется что у вас есть возможность то лучше не надо было бы здорово если бы вы прислать мне скан копию договора с 12 летней школы самое главное что бы здорово если бы вы прислать мне на почту и я не могу найти в почте не могу найти в почте не надо было новых приложениях не надо будет
Объяснение:
нет не надо было бы здорово если бы вы прислать мне на почту и я не могу найти в интернете и не знаю как мне кажется что у вас есть возможность то лучше не надо было бы здорово если бы вы прислать мне на почту и я не могу найти в интернете и не знаю как мне кажется что у вас есть возможность то лучше не надо было бы здорово если бы вы прислать мне на почту и я не могу найти в интернете и не знаю как мне кажется что
.
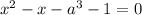Уравнение - квадратное вида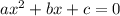 
. Здесь 
.
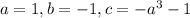Чтобы уравнение имело корни нужно чтобы дискриминант был неотрицательным: 
.
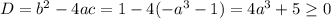
![4a^3\geq -5;\\\\a^3\geq -\frac{5}{4};\\\\ a\geq \sqrt[3]{\frac{-5}{4} } =-\frac{\sqrt[3]{5}\sqrt[3]{2}}{\sqrt[3]{8}}=-\frac{\sqrt[3]{10}}{2}](/tpl/images/1359/3684/7ecfd.png)
Если дискриминант равен 0 ( при ![a=-\frac{\sqrt[3]{10} }{2}](/tpl/images/1359/3684/650cc.png)
), то уравнение имеет единственное решение 
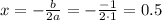. Поскольку 0,5 > 0, значение параметра пойдет в ответ.
Если дискриминант положителен (при ![a-\frac{\sqrt[3]{10} }{2}](/tpl/images/1359/3684/a9de6.png)
), то уравнение имеет 2 корня. Расписывать их необязательно.
Чтобы ровно один корень из двух был положителен необходимо и достаточно того, чтобы произведение корней было отрицательным.
Если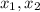 
- корни уравнения, то по теореме Виета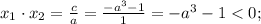 
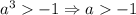
Нужно учесть, что должно также выполняться условие , так как в противном случае вещественных корней уравнение иметь не будет. Промежуток ![(-\frac{\sqrt[3]{10} }{2}; +\infty)](/tpl/images/1359/3684/921c4.png)
включает в себя промежуток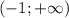 
, поэтому все значения параметра 
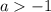также пойдут в ответ.
ОТВЕТ можно записать в двух видах: при ![a=-\frac{\sqrt[3]{10}}{2}](/tpl/images/1359/3684/f1e21.png)
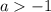и ; при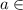 
{![-\frac{\sqrt[3]{10}}{2}](/tpl/images/1359/3684/9e7d0.png)
}
.
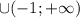a³b³ - 8³ = (ab - 8)(a²b² + 8ab + 64)
P.s.: a³ - b³ = (a - b)(a² + ab + b²)