(-∞ ;-3) => функция выпукла;
(-3; +∞) => функция вогнута;
(-∞ ;-6) <=> f'(x) > 0 => функция возрастает;
(-6; 0) <=> f'(x) < 0 => функция убывает;
(0; +∞) <=> f'(x) > 0 => функция возрастает ;
Объяснение:
1. Находим интервалы возрастания и убывания. Первая производная.
f'(x) = 3x2+18x
или
f'(x)=3x(x+6)
Находим нули функции. Для этого приравниваем производную к нулю
x(x+6) = 0
Откуда:
x1 = 0
x2 = -6
(-∞ ;-6) <=> f'(x) > 0 => функция возрастает;
(-6; 0) <=> f'(x) < 0 => функция убывает;
(0; +∞) <=> f'(x) > 0 => функция возрастает ;
В окрестности точки x = -6 производная функции меняет знак с (+) на (-). Следовательно, точка x = -6 - точка максимума. В окрестности точки x = 0 производная функции меняет знак с (-) на (+). Следовательно, точка x = 0 - точка минимума.
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.
f''(x) = 6x+18
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
6x+18 = 0
Откуда точки перегиба:
x1 = -3
(-∞ ;-3) => функция выпукла;
(-3; +∞) => функция вогнута;
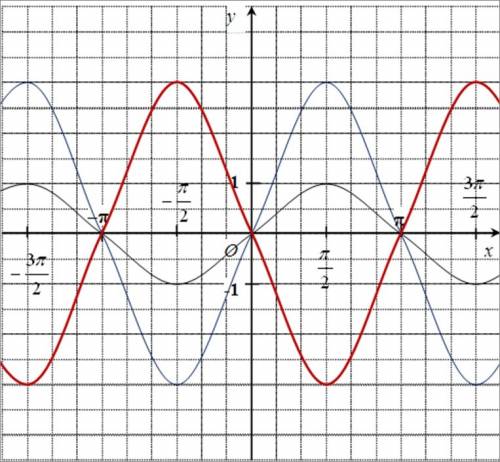
Для построения графика функции у = -3sinx поступаем так:
1) строим график функции у = sinx, зная, что эта функция нечетная и ее график проходит через точки (0;0), (π/2; 1), (π;0) и (3π/2; -1) и т.д. и затем строим его часть, симметричную относительно начала координат, учитывая, что нужный график - это граафик нечетной функции (на рис. - черного цвета);
2) затем строим график функции у = 3sinx, учитывая, что он как бы "растягивается" вдоль оси Оу в 3 раза (на рис. -синего цвета);
3) затем строим график функции у = -3sinx, отражая его симметрично относительно оси Ох (на рис. - красного цвета).