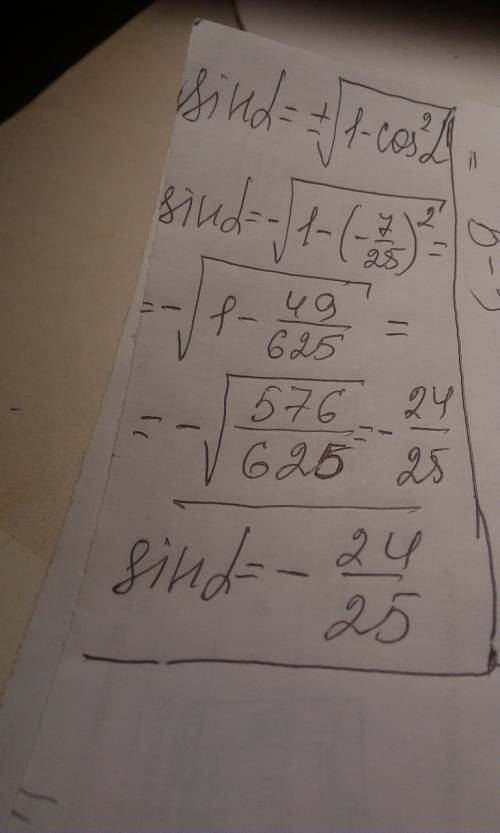
№408 (3-6)
3) (2x+1)²-(x+1)×(x-7)≤5
4x²+4x+1-x²+6x+7≤5
3x²+10x+8≤5
3x²+9x+x+8-5≤0
3x²+9x+x+3≤0
3x×(x+3)+x+3≤0
(x+3)×(3x+1)≤0
x≤-3 — пустое множество
x≥-1/3 — пустое множество
x≥-3
x≤-1/3
ответ: [-3; -1/3]
4) 5x×(x+4)-(2x-3)×(2x+3)>30
5x²+20x-4x²-9>30
x²+20x-9>30
x²+20x-39>0
x1=-10+√139
x2=-10-√139
ответ: (-∞; -10-√139)U(-10+√139; +∞)
5)(3x-7)×(x+2)-(x-4)×(x+5)>30
3x²-x-14-x²-x+20>30
2x²-2x+6-30>0
2x²-2x-24>0 — можем поделить на 2
x²-x-12>0
(x+3)×(x-4)>0
x>-3 →↓
x>4 →(4;+∞)
x<-3 →(-∞;-3)
x<4 →↑
ответ: (-∞;-3)U(4;+∞)
Я напишу только ответ, прости, устал печатать! И задерживать сильно не буду
6) ответ: [-13/3; 1]
№409 — Всё также!
Расстояние между А и В равно 32 км.
Объяснение:
В 9.00 велосипедист выехал из А в В. В 11.30 он отправился в обратный путь из в в А, отдохнув полчаса (30 мин). То есть на путь из А в В и отдых он затратил 11.30 - 9.00 = 2.30 (два часа 30 минут). Если вычесть время отдыха, то получим время, которое затратил велосипедист на путь из А в В: 2 ч 30 мин - 30 мин = 2 ч.
Пусть х - расстояние от А до В, тогда
х : 2 = 0,5х - скорость велосипедиста в км/ч.
Второй известный отрезок времени 13.00 - 11.30 = 1.30 (1 час 30 мин = 1,5ч) затратил велосипедист на расстояние (х - 8) км на обратном пути из В в А.
Он ехал с прежней скоростью, поэтому х - 8 = 0,5х · 1,5
х - 8 = 0,75х
0,25х = 8
х = 32 (км)