Решением данной системы является пара чисел: 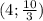 .
.
Объяснение:
Перед нами система уравнений с двумя неизвестными:
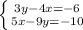
Данную систему уравнений проще решить, используя метод исключения одной переменной. Для этого домножим обе части первого уравнения на 3:
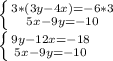
Теперь, сложим оба уравнения данной системы, чтобы избавиться от переменной y. Найдем x, путем упрощения обычного уравнения:
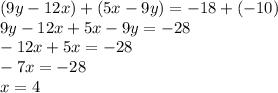
Теперь подставим данное значение в первое уравнение системы, чтобы найти y:
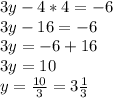
Получили ответ, что решением данной системы является пара чисел: 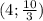
Пусть A1 — центр вписанной окружности ∆ SBC, B1 — центр вписанной окружности ∆ SAC, AA1 пересекается с A, A1, B1, B лежат в одной плоскости, значит прямые AB1 и BA1 пересекаются на ребре SC. Пусть точка пересечения этих прямых — p. Так как Ap и Bp — биссектрисы углов A и B, то . Но тогда AC • BS = BC • AS, отсюда , следовательно биссектрисы углов S в ∆ ASB и C в ∆ ACB пересекаются на ребре AB, т.е. точки S, C и центры вписанных окружностей ∆ ASB и ∆ ACB лежат в одной плоскости. Отсюда следует, что отрезки, соединяющие вершины S и C с центрами вписанных окружностей противолежащих граней, пересекаются.
1. Целыми выражениями называются: а) все числовые выражения; б) выражения с переменными, содержащие операции сложения, вычитания, умножения и возведения переменных в натуральную степень.
Примеры целых выражений:
Выражения не являются целыми, так как они содержат операции возведения в целую отрицательную степень и деления на переменную.
2. Одночлены и многочлены являются целыми выражениями.
3. Если в выражении с переменными, кроме операций сложения, умножения, вычитания и возведения в натуральную степень, производится и операция деления на переменную, то такие выражения называются дробными выражениями.
Например, — дробные выражения.