1) Обозначим первую цифру задуманного числа х, а вторую - у. Выполнив указанные действия, получим:
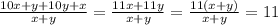
Т.е., всегда будет получаться 11.
2) Признак делимости на 3: на три делятся те числа, сумма цифр которых делится на 3.
Данное число (10^n+317) будет состоять из единицы, n нулей, тройки, единицы и семёрки. Сумма цифр равна 1+3+1+7 = 12.
12 делится на 3, значит, и число 10^n+317 тоже делится на 3, ЧТД
Аналогично, признак делимости на 9: на 9 делятся те числа, сумма цифр которых делится на 9.
10^n состоит из единицы и n нулей. Если от него отнять 1, оно будет состоять из девяток. Соответсвенно, сумма цифр этого числа поделится на 9, ЧТД.
Дана система:
{3x+4y=-2
{2x-7y=6.
Применим сложения.
{3x+4y=-2, х 2 {6x + 8y = -4
{2x-7y=6, х(-3) {-6x + 21y = -18
29y = -22. отсюда у = -22/29.
Подставляем во второе уравнение, выраженное относительно х:
2x-7y=6,
х = (6 + 7у)/2 = (6 + 7*(-22/29))/2 = (174 - 154)/(2*29) = 10/29.