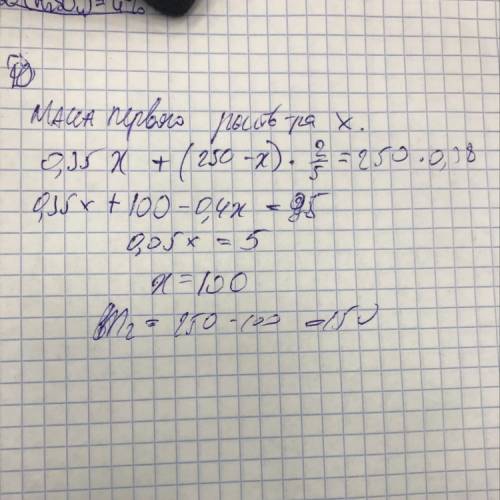
Объяснение:
Объяснение:
1. Какие из точек принадлежат графику функции у=2х-3?
3)Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
А(-1;-5)
-5=2*(-1)-3
-5= -5, принадлежит.
С(-4;7)
7=2*(-4)-3
7≠ -11, не принадлежит
В(0;3)
3=2*0-3
3≠ -3, не принадлежит.
D(2,5; 2)
2=2*2,5-3
2=2, принадлежит.
2. Графиком некоторой функции является ломанная ABC, где А (-6; 5), В (-2; -3), С (4; 3):
а)Постройте график данной функции;
б) Найдите значение функции, если значение аргумента равно -4 и 3; в)Найдите значение аргумента, если значение функции равно -3 и 2.
а)по заданным точкам строим график.
б)согласно графика при х= -4 у=1
согласно графика при х= 3 у=2
в)согласно графика при у= -3 х= -2
согласно графика при у=2 х=3.
3. На рисунке изображен график функции у=f(х).
Пользуясь графиком, найдите:
а) область определения функции;
б) область значений функции;
в)значения х, при котором у=2;
г) значение у, при котором х=3;
д) значение аргумента, при которых значения функции отрицательны;
е) значение аргумента, при которых значения функции положительны.
а)область определения это значения х, при которых построен этот график, от -2 до 7, ось Ох, обозначается х∈[-2, 7]
Скобки квадратные, потому что числа -2 и 7 входят в область определения.
б)область значений это значения у, при которых построен этот график, от -2 до 4,8, ось Оу, обозначение E(у) [-2, 4,8]
Скобки квадратные, потому что числа -2 и 4,8 входят в область значений.
в)у=2
Проводим мысленно прямую через точку у=2, параллельно оси Ох.
Есть три точки пересечения этой прямой с графиком, опускаем вниз перпендикуляры и записываем значения х:
х₁= -1,5 х₂=2,3 х₃=6
г)х=3
Проводим мысленно прямую через точку х=3, параллельно оси Оу. Есть одна точка пересечения с графиком, опускаем перпендикуляр влево, на ось Оу, у=3.
д)найти х, при которых у<0.
У<0 (ниже оси Ох) при х от 6,5 до 7 х∈[6,5, 7] Скобки квадратные, потому что числа 6,5 и 7 входят в область значений.
е)найти х, при которых у> 0.
У>0 (выше оси Ох) при х от -2 до 6,5 х∈[-2, 6,5] Скобки квадратные, потому что числа -2 и 6,5 входят в область значений.
1) Найди дискриминант квадратного уравнения 8x²+4x+12=0.
D = b² - 4ac = 16 - 4·8·12 = 16 - 384 = -368.
2) Найди корни квадратного уравнения x²+7x+12=0.
По т., обратной к т. Виетта, имеем х₁ = -4; x₂ = -3.
3) Реши квадратное уравнение 2(5x−15)²−7(5x−15)+6=0.
Рациональным будет метод введения новой переменной.
Пусть 5x−15 = t, тогда имеем:
2t²−7t+6=0; D = b² - 4ac = 49 - 4·2·6 = 49 - 48 = 1; √D = 1
t₁ = (7 + 1)/4 = 2; t₂ = (7 - 1)/4 = 1,5.
Возвращаемся к замене:
5x−15 =2; 5x = 2 + 15; 5x = 17; x = 17/5; x₁ = 3,4.
5x−15 = 1,5; 5x = 1,5 + 15; 5x = 16,5; x = 16,5/5; x₂ = 3,3.
ответ: 3,4; 3,3.
4)Найди корни уравнения −8,9(x−2,1)(x−31)=0.
x−2,1 = 0 или x−31 = 0.
х₁ = 2,1 х₂ = 31.
ответ: 2,1; 31.
5) Сократи дробь (x−4)²/(x²+2x−24) = (x−4)²/((x + 6)(x − 4)) = (х - 4)/(х + 6).
Полученная дробь: (х - 4)/(х + 6).
6)Сократи дробь (5x²−32x+12)/(x³−216).
5x²−32x+12 = 0; D = b² - 4ac = 1024 - 480 = 784; √D = 28.
x₁ = (32 + 28)/10 = 6; x₂ = (32 - 28)/10 = 0,4
Имеем: (5x²−32x+12)/(x³−216) = ((x - 6)(5x - 2))/((x - 6)(x² + 6x + 36)) =
= (5x - 2)/(x² + 6x + 36).
7) Разложи на множители квадратный трехчлен x² + 8x + 15.
x² + 8x + 15 = 0; x₁ = -3; x₂ = -5.
имеем, x² + 8x + 15 = (x + 3)(x + 5).