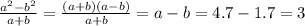
Для составления уравнения плоскости используем формулу:
x - xA y - yA z - zA
xB - xA yB - yA zB - zA
xC - xA yC - yA zC - zA
= 0
Для плоскости АВС подставляем данные.
Подставим данные и упростим выражение:
x - 2 y - 0 z - 0
5 - 2 3 - 0 0 - 0
0 - 2 1 - 0 1 - 0
= 0
x - 2 y - 0 z - 0
3 3 0
-2 1 1
(x - 2)(3·1-0·1) - (y - 0)(3·1-0·(-2)) + (z - 0)(3·1-3·(-2)) = 0
3 x - 6 + (-3) y - 0 + 9 z - 0 = 0
3x - 3y + 9z - 6 = 0 , или, сократив на 3, получаем уравнение плоскости АВС: x - y + 3z - 2 = 0.
Аналогично для плоскости АВД.
x - 2 y - 0 z - 0 = 0
5 - 2 3 - 0 0 - 0
(-2) - 2 (-4) - 0 1 - 0
x - 2 y - 0 z - 0 = 0
3 3 0
-4 -4 1
(x - 2)(3 ·1-0 ·(-4)) - (y - 0)(3 ·1-0 ·(-4)) + (z -0)(3 ·(-4) -3·(-4) ) = 0
3(x - 2) + (-3) (y - 0) + 0(z - 0) = 0
3x - 3y - 6 = 0 или, сократив на 3, получаем уравнение плоскости АВД:
x - y - 2 = 0.
Угол между плоскостями определяем по формуле:
cos α = |A1·A2 + B1·B2 + C1·C2|
√(A1² + B1² + C1²)*√(A2² + B2² + C2²).
Подставим данные: АВС: x - y + 3z - 2 = 0, АВД: x - y - 2 = 0.
cos α = |1*1 + (-1)*(-1) + 3*(-2)|/ (√(1 + 1 + 9)*√(1 + 1 + 4)) = 0,4264.
α = 1,1303 радиан или 64,761 градус .
Объяснение:
Пусть братьям а, aq и aq² лет. ⇒
Они получат соответственно х, xq и xq² рублей.
Через 3 года им будет а+3, aq+3 и aq²+3 лет, причём старшему будет вдвое больше лет, чем младшему:
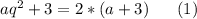
Через 3 года младший брат получит х+105 рублей, а средний - xq+15. Таким образом старший брат получит:
(x+xq+xq²)-(x+105)-(xq+15)=x+xq+xq²-x-105-xq-15=xq²-120.
Так как братья делят деньги пропорционально их возрасту ⇒

Подставляем уравнение (1) в уравнение (3):

Преобразуем уравнение (1):
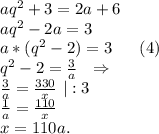
Теперь уравнение (2) можно переписать:
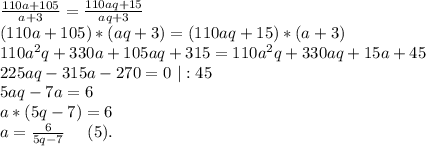
Подставляем уравнение (5) в уравнение (4):
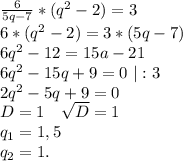
q₂=1 - посторонний корень, так как тогда братьям будет одинаковое количество лет и никто не сможет стать через 3 года вдвое старше. ⇒
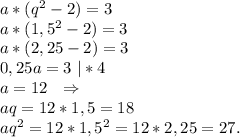
ответ: старшему брату 27 лет.