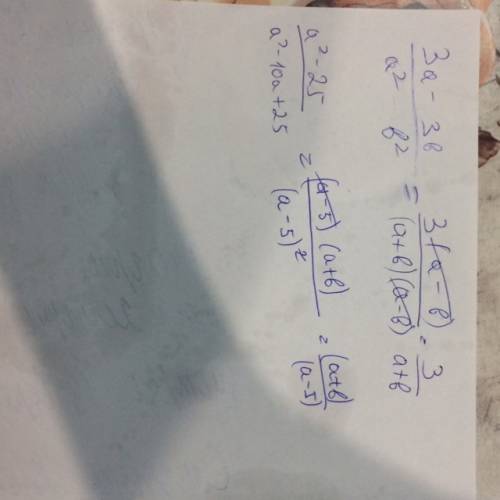
Объяснение:
1) 2х + 1 = 3х - 4
Перенесём известные слагаемые в одну сторону, неизвестные в другую:
2x-3x = -4-1
-x=-5
Делим обе части на множитель при переменной x (-1)
x=5
ответ: 5.
2) 1,6(5х – 1) = 1,8х – 4,7
Раскроем скобки:
8x-1,6=1,8х-4,7
Перенесём известные слагаемые в одну сторону, неизвестные в другую:
8х-1,8х=-4,7+1,6
6,2х=-3,1
Делим обе части на множитель при переменной x (6,2)
х=-0,5
ответ: -0,5.
3) - 2х + 1 = - х - 6
Перенесём известные слагаемые в одну сторону, неизвестные в другую:
-2х+х=-6-1
-х=-7
Делим обе части на множитель при переменной x (-1)
х=7
ответ: 7.
-
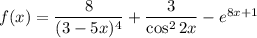
Совокупность всех первообразных функции 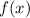 называют неопределенным интегралом:
называют неопределенным интегралом:
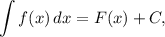
где 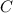 — произвольная постоянная.
— произвольная постоянная.
Тогда 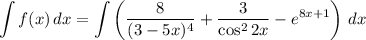
Теорема: если функции  и
и 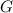 являются соответственно первообразными функций
являются соответственно первообразными функций 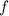 и
и 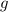 на промежутке
на промежутке 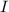 , то на этом промежутке функция
, то на этом промежутке функция 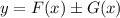 является первообразной функции
является первообразной функции 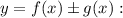
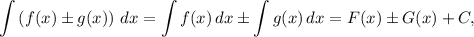
где 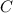 — произвольная постоянная.
— произвольная постоянная.
Тогда 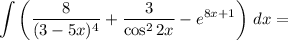
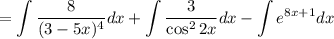
Теорема: если функция 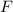 является первообразной для функции
является первообразной для функции 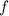 на промежутке
на промежутке 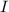 , а
, а 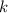 — некоторое число, то на этом промежутке функция
— некоторое число, то на этом промежутке функция 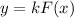 является первообразной функции
является первообразной функции 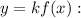
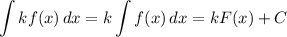
Тогда 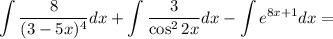
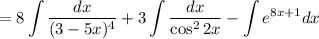
Теорема: если функция  является первообразной для функции
является первообразной для функции  на промежутке
на промежутке 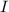 , а
, а 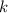 — некоторое число, отличное от нуля, то на соответствующем промежутке функция
— некоторое число, отличное от нуля, то на соответствующем промежутке функция 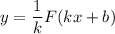 является первообразной функции
является первообразной функции 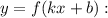
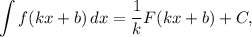
где 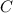 — произвольная постоянная.
— произвольная постоянная.
Найдем каждый интеграл по отдельности:
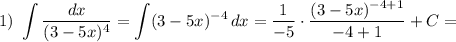
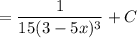
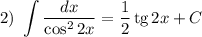
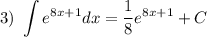
Получаем: 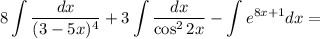
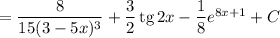
Таким образом, общий вид первообразных для функции 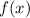 имеет вид:
имеет вид:
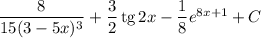
ответ: 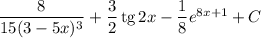
Использованные формулы интегрирования:
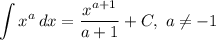
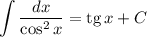
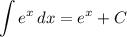
= =
а²-в² (а-в)(а+в) а+в
а²-25 (а-5)(а+5) а+5
= =
а²-10а+25 (а-5)² а-5