a)х∈(6, +∞);
б)х∈(1, +∞).
Объяснение:
Решить систему неравенств:
а) 6х – 24 > 0
-2х + 12 < 0
Первое неравенство:
6х – 24 > 0
6х>24
х>4
х∈(4, +∞) интервал решений первого неравенства.
Неравенство строгое, скобки круглые.
Второе неравенство:
-2х + 12 < 0
-2х<-12
х>6 знак меняется
х∈(6, +∞) интервал решений второго неравенства.
Неравенство строгое, скобки круглые.
Теперь нужно на числовой оси отметить оба интервала, чтобы найти пересечение, то есть, такое решение, которое подходит двум данным неравенствам.
Пересечение (решение системы неравенств) х∈(6, +∞)
б) 3(х-4) - 4(х+3) ≤ 0
3х + 2(3х-2) > 5
Первое неравенство:
3(х-4) - 4(х+3) ≤ 0
3х-12-4х-12<=0
-x<=24
x>= -24 знак меняется
х∈[-24, +∞) интервал решений первого неравенства.
Неравенство нестрогое, скобка квадратная.
Второе неравенство:
3х + 2(3х-2) > 5
3х+6х-4>5
9x>5+4
9x>9
x>1
х∈(1, +∞) интервал решений второго неравенства.
Неравенство строгое, скобки круглые.
Теперь нужно на числовой оси отметить оба интервала, чтобы найти пересечение, то есть, такое решение, которое подходит двум данным неравенствам.
Пересечение (решение системы неравенств) х∈(1, +∞)
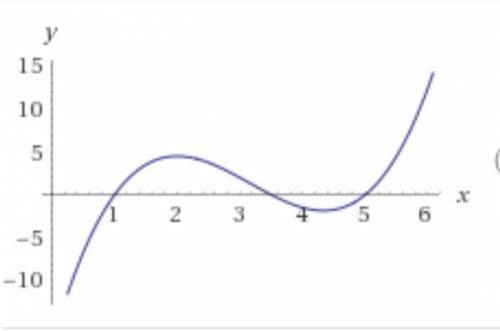
Будем считать, что надо найти корни заданного кубического выражения.
y=x^3-9,5x^2+26x-17,5 = 0.
Один корень явно виден - это х = 1.
Разделим многочлен на (х - 1):
x^3 - 9,5x^2 + 26x - 17,5 |x - 1
x^3 - x^2 x^2 - 8,5x + 17,5
-8,5x^2 + 26x
-8,5x^2 + 8,5x
-17,5x - 17,5
-17,5x - 17,5
0
Полученный квадратный трёхчлен разложим на множители, найдя его корни.
Решаем уравнение x^2 - 8,5*x + 17,5=0.
Ищем дискриминант:
D=(-8.5)^2-4*1*17.5=72.25-4*17.5=72.25-70=2.25;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(-(√2,25-8,5))/(2*1)=(1,5-(-8,5))/2=(1,5+8,5)/2=10/2=5;
x_2=(-√2,25-(-8,5))/(2*1)=(-1,5-(-8,5))/2=(-1,5+8,5)/2=7/2=3,5.
ответ: имеем три корня х = 1, х = 3,5 и х = 5.
Далее при приведении подобных и сократятся и останутся 4 слагаемых: