1. Упростите выражение
-12х+3ху-2(х+3ху)
-12x+3xy-2x-6xy= -14x-3xy
2. Из предложенных четырех пар чисел выбрите ту, которая является недопустимой для алгебраической дроби
2а²+3аb-b³
=b²-9a²>0 (b-3a)(b+3a) >0 видно что (3;1) так как =0
b²-9a²
3. Какое из четырех равенств не является тоджеством:
1. х³-8=(х-2)(х²+2х+4) Верно так как это разность кубов
2. х³+27=(х+3)(х²+3х+9) нет
3. х²-8х+16=(х-4)² да
4. х²+4ху+4у²=(х+2у)² да
(72²-28²)/(61²-39²) =(72-28)(72 + 28 )/ (61-39)(61+39)=2
4а⁷b¹⁵-4a⁵b¹⁷ 4a⁵b¹⁵(a²-b²) 2ab¹¹ (a-b)(a+b) -2ab¹¹ (a+b) = -2*3*-1*2=12
= = =
2a⁴b⁵-2a⁵b⁴ 2a⁴b⁴(b-a) -(a-b)
6.Преобразовав линейное уравнение 2х+3у-3=0 к виду линейной функции у=кх+м, найдите ее угловой коэффициент.
3y=3-2x
y=-2x/3+1
ответ -2/3
7.Найдите наибольшее значение функции у=3х-1 на отрезке [0,⅓]
f(0) = -1
f(1/3)=0
значит 0
8. Дана фунция у=f(x), где
| x², если -3≤ х ≤ 0;
|3x-1, если 0<х<2
|х, если х ≥ 2
Чему равно f(2)?
2 попадает на интервал x значит равна y=2
9.Какая из предложенных четырех пар чисел (x;y) является решением системы уравнений
|3x+y=7
|5x-8y=31
|y=7-3x
|5x-56+24x=31
|29x=87
|x=3
|y=-2
Объяснение:
Рассмотрим числа x y z:
1) Если все положительные x y z, то и результат будет положительный.
2) Если одно из значений отрицательно, то каждая дробь будет отрицательной и ответ будет отрицательный:
К примеру возьмём x=10, y=10, z=-10
3)Если два отрицательных, то ответ будет положительным (аналогично 2 примеру)
4)и наконец 3 отрицательных, все дроби отрицательные⇒ответ отрицательный.
Т.к. наше выражение =3>0, то нас устраивают случаи 1) и 3).
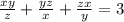
Преобразуем равенство, умножив на 2xyz(x,y,z≠0):
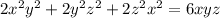
5) Отсюда видно что если числа x, y, z являются решением, то, изменив знак у любых двух чисел из этой тройки, мы снова получим решение уравнения. Поэтому достаточно рассмотреть положительные решения, а оставшиеся получить путем чередования двух минусов.
Рассмотрим левую часть уравнения:
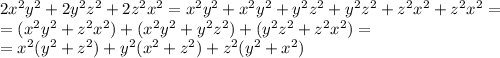
Помним, что квадрат числа неотрицательное число, поэтому:
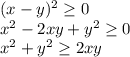
Значит наше выражение:
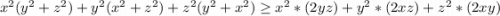
Вспомним что изначальное выражение равнялось 6xyz:
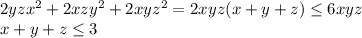
Т.к. x,y,z положительные, то в натуральных числах есть одно решение: (1,1,1).
Учитывая 5 пункт получаем 4 решения:
(1,1,1), (-1;-1;1), (-1;1;-1), (1;-1;-1)
2*6-(-5)
12-(-5)=7