Найдем сначала уравнение секущей:
Она проходит через две точки:х1=-1, у1 = 2*(-1)^2 = 2
и х2 = 2, у2 = 2*2^2 = 8
Ищем уравнение секущей в виде: y=kx+b
Подставим сюда две наши точки и решим систему, найдем k:
-k+b=2
2k+b=8 Вычтем из второго первое: 3k = 6, k= 2.
Наша искомая касательная должна быть параллельна секущей, значит имее такой же угловой коэффициент. k=2
Найдем точку касания, приравняв производную нашей ф-ии двум:
Y' = 4x = 2
x = 1/2
Уравнение касательной к ф-ии в т.х0:
у = у(х0) + y'(x0)(x-x0)
Унас х0 = 1/2, у(1/2) = 2*(1/4) = 1/2, y'(1/2)= 2.
Тогда получим:
у = 1/2 + 2(х - 1/2)
у = 2х -0,5 - искомое уравнение касательной.
Допустим, что 
. Тогда имеем уравнение 
, не имеющее решений, поскольку в левой части число неположительное, а в правой - положительное, т.е. левая часть никак не может быть равна правой. Т.е.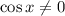 
Преобразуем правую часть:
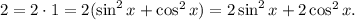
Перенесем все влево с противоположным знаком:
Поскольку 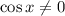, можем разделить обе части уравнения на 
. В итоге имеет равносильное исходному уравнение
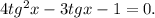
Заметим, что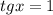 
является корнем уравнения относительно тангенса. Тогда по теореме Виета второй корень равен 
.
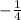Соответственно, имеем два случая: или 
или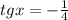 
.
1 случай.
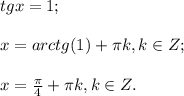
2 случай.
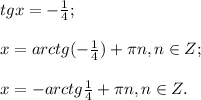
Имеем две серии корней.
ОТВЕТ: π/4 + πk, k ∈ Z; -arctg(1/4) + πn, n ∈ Z.
Выразим данное число А как:
А1 = 3а + 1; А2 = 3а + 2.
Тогда A^2:
(A1)^2 = (3a + 1)^2 = 9a^2 + 6a + 1 = 3(3a^2 + 2a) + 1;
(A2)^2 = (3a + 2)^2 = 9a^2 + 12a + 4 = 3(3a^2 + 4a + 1) + 1.
Квадрат данного числа, уменьшенный на 1:
(А1)^2 - 1 = 3(3a^2 + 2a); (A2)^2 - 1 = 3(3a^2 + 4a + 1).
Утверждение доказано.