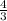, значит![27^ \frac{4}{3} = \sqrt[3]{27^4} =( \sqrt[3]{27} )^4=3^4 =81](/tpl/images/0797/6552/8db9a.png)
Формула объема призмы: Площадь основания (Sосн.) умножить на высоту (h), тобишь:
Vпризмы=Sосн.*h
Площадь основания правильного шестиугольника равна: три корня из трех на два умножить на сторону в квадрате(a), тобишь:
Sосн.=3√3/2*a^2
Из текста задачи ясно, что объем не изменился. Получаем: V1=V2, а сторона основания второй призмы в два раза меньше, и обозначив сторону первой за a, сторону второй обозначим через a/2.
Приравниванием формулы объема первой и второй призмы,обозначаем искомую высоту через x и получаем уравнение:
3√3/2*a^2*24=3√3/2*a^2/4*x
Делим обе части уравнения на 3√3/2 и получаем:
a^2*24=a^2/4*x
Чтобы избавится от знаменателя во второй части домнажаем обе части на 4:
96*a^2=a^2x
x=96a^2/a^2
В результате a^2 сокращается и остается 96:
x=96.
ответ:96 см.
ответ: 9
Объяснение:
Пусть x- неизвестное однозначное число
Найдем процент на которое увеличилось число , после увеличения его на 12 : 12*100% / x .
Найдем на сколько нужно увеличить полученное число x+ 12 :
( (x+12) * 12*100%/x)/100% = 12* (x+12)/x Уравнение имеет вид:
(x+12) + 12*(x+12)/x=49 (x ≠ 0)
x*(x+12) +12*(x+12)=49*x
x^2-25*x+144=0
D= 25^2 -4*144= 625-576=49=7^2
x= (25+-7)/2
x1=16 - не подходит , поскольку данное число двузначное
x2=9 - число однозначно
ответ :9
27^1,(3) = 27^(1(целая)1/3) = 27 * 27^1/3 = 27 * (3³)^1/3 = 27*3 = 81