ответ: 21/29.
Объяснение:
Событие А — лампочка окажется стандартной;
H₁ — лампочка изготовлена из первого завода;
H₂ — лампочка изготовлена из второго завода.
Из условия: P(H₁) = 70%/100% = 0.7; P(H₂) = 30%/100% = 0.3
P(A|H₁) = 90/100 = 0.9
P(A|H₂) = 80/100 = 0.8
По формуле полной вероятности, вероятность того, что лампочка окажется стандартной равна:
P(A) = P(H₁)P(A|H₁) + P(H₂)P(A|H₂) = 0.9 * 0.7 + 0.8 * 0.3 = 0.87
По формуле Байеса, вероятность того, что стандартная лампочка изготовлена на первом заводе, равна:
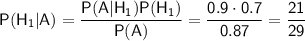
ответ:Определим моменты времени, когда мяч находился на высоте ровно четыре метра. Для этого решим уравнение :
h(t)=-1,1+20t-10t^2
-1,1+20t-10t^2≥ 4
10t^2 - 20t + 4 + 1,1 ≤ 0
10t^2 - 20t + 5,1 ≤ 0
D = 20^2 - 4 *10*5.1 = 400 - 204 =196 =16
t1 = (20+16)/2*10 = 1,8
t2 = (20-16)/2*10 = 0,2
поскольку по условию задачи мяч брошен снизу вверх, это означает, что в момент времени (с) мяч находился на высоте 4 метра, двигаясь снизу вверх, а в момент времени (с) мяч находился на этой высоте, двигаясь сверху вниз. Поэтому он находился на высоте не менее 4 метров 1,8 − 0,2 = 1,6 секунды.
Объяснение: