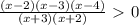1.решите двойные неравенства а) -4 больше или равно 3х +2 больше или равно 6 б) -3< 5х-2< 4 2.область определения функции а) f(х)=корень -х^2 +5х+14 б)f(х)=корень -2^2+5х-2 1.решите неравенства а)7х+3х> 5(х-4)+1 б)2х^2+13х-7> 0 в)х^2+7х\х-3 < 0 г)х^2+9х\х-2< 0 д)3х^2+5х-8 больше или равно 0 4.система неравенств 3х^2-х> 0 \х< 0

👇

Ответ:

дима22819

02.06.2020

Вот решение 1-ого задания:
1.решите двойные неравенства а) -4 больше или равно 3х +2 больше или равно 6 б) -3< 5х-2< 4 2.

4,8(67 оценок)

Открыть все ответы

Ответ:

zhovnovich

02.06.2020

Первый из трех обозначим b1
следующий: b1*q
третий: b1*q² (q > 0)
b1 + b1*q + b1*q² = 21
b1*(1+q+q²) = 21 ---> b1 = 21 / (1+q+q²)
(1 / b1) + (1 / (b1*q)) + (1 / (b1*q²)) = 7/12
(1 / b1)*(1 + (1/q) + (1/q²)) = 7/12
((1+q+q²) / 21)*((q²+q+1) / q²) = 7/12
(1+q+q²)² = (7/12) * 21q²
((1+q+q²) / q)² = 49/4
(1+q+q²) / q = 7/2 или (1+q+q²) / q = -7/2
2+2q+2q² = 7q или 2+2q+2q² = -7q
2q²-5q+2 = 0 или 2q²+9q+2 = 0
D=25-16=3² D=81-16=65
q1 = (5-3)/4 = 0.5 q3 = (-9-√65)/4 < 0
q2 = (5+3)/4 = 2 q4 = (-9+√65)/4 < 0
1) q = 1/2 --- убывающая последовательность
b1 = 21 / (1+0.5+0.25) = 21 / 1.75 = 12
b2 = 12*0.5 = 6
b3 = 6*0.5 = 3 их сумма = 21
(1/12) + (1/6) + (1/3) = (1/12) + (2/12) + (4/12) = 7/12
2) q = 2 --- возрастающая последовательность
b1 = 21 / (1+2+4) = 3
b2 = 3*2 = 6
b3 = 6*2 = 12 их сумма = 21
(1/12) + (1/6) + (1/3) = (1/12) + (2/12) + (4/12) = 7/12

4,7(62 оценок)

Ответ:

prepelitsa

02.06.2020

$\frac{(x-2)(x-3)(x-4) }{ (x+3)(x+2)} \ \textgreater \ 0$
Находим нули функции:
$\frac{(x-2)(x-3)(x-4) }{ (x+3)(x+2)}=0 \\ \left \{ {{(x-2)(x-3)(x-4)=0} \atop {(x+3)(x+2) \neq 0}} \right. \\ \\ x=2 \\ x=3 \\ x=4 \\ x \neq -3 \\ x \neq -2$

Обозначаем нули на ОДЗ и находим знак функции f (x) в каждом промежутке, на которые разбиваем ОДЗ
(Для того чтобы найти знак мы берем любое число, которое принадлежит данном промежутке, например на промежутке (-2; 2) можно взять число 0, и подставляем его в неравенство вместо х и тогда высчитываем, если получается отрицательное число, то ставим знак минус, а если положительное, то плюс)
__-____-3___+__-2___-___2____+___3__-___4__+_>x

Так как по условию нужно найти числа, которые больше нуля, то промежутки имеющих знак плюс и являются ответом для неравенства.

x∈(-3;-2)∨(2;3)∨(4; +∞)

4,8(80 оценок)

Это интересно:

Здоровье

22.01.2023

Как сделать мешочек с кукурузой: всё, что нужно знать...

Питомцы-и-животные

21.04.2022

Как выращивать кроликов ради мяса или шерсти...

Хобби-и-рукоделие

07.07.2021

Как сделать светящуюся палочку: пошаговая инструкция...

Дом-и-сад