В решении.
Объяснение:
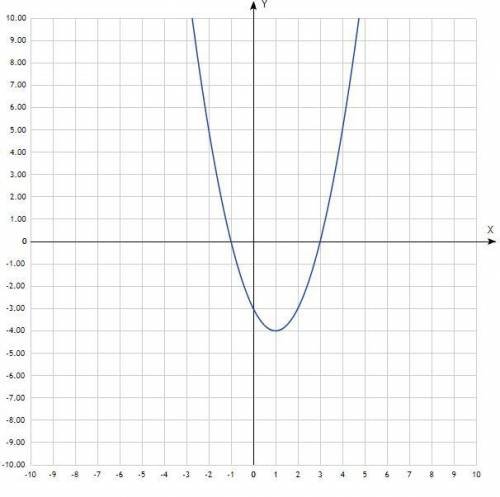
Побудувати графік функції
у = х² - 2x – 3.
Построить график функции у = х² - 2x – 3. Квадратичная функция, график - парабола со смещённым центром, ветви направлены вверх. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3 4 5
у 12 5 0 -3 -4 -3 0 5 12
Вказати:
1) проміжок, в якому функція зростає;
Согласно графика, функция возрастает на промежутке х∈(1; +∞).
2) множину розв'язків нерівності х² - 2x - 3 ≤ 0.
Приравнять к нулю и решить квадратное уравнение при графика:
Уравнение квадратичной функции, график - парабола, ветви пересекают ось Ох в точках х= -1 и х= 3.
Значения корней известны, решения неравенства: х∈[-1; 3].
Неравенство нестрогое, скобки квадратные.
В решении.
Объяснение:
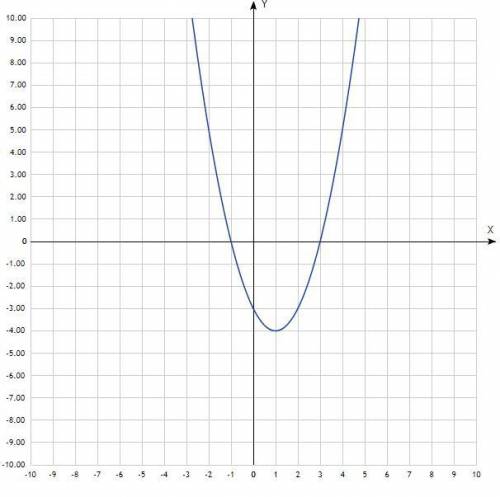
Побудувати графік функції
у = х² - 2x – 3.
Построить график функции у = х² - 2x – 3. Квадратичная функция, график - парабола со смещённым центром, ветви направлены вверх. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -3 -2 -1 0 1 2 3 4 5
у 12 5 0 -3 -4 -3 0 5 12
Вказати:
1) проміжок, в якому функція зростає;
Согласно графика, функция возрастает на промежутке х∈(1; +∞).
2) множину розв'язків нерівності х² - 2x - 3 ≤ 0.
Приравнять к нулю и решить квадратное уравнение при графика:
Уравнение квадратичной функции, график - парабола, ветви пересекают ось Ох в точках х= -1 и х= 3.
Значения корней известны, решения неравенства: х∈[-1; 3].
Неравенство нестрогое, скобки квадратные.
а) 3х(3х-1)=0
х(2х-1)=0
х=0
2х-1=0
х=1/2
х1=0,х2=0,5
б)х(х+9)
х=0
х+9=0
х=-9
х1=-9,х2=0
в)x^2=36
x=-6,x=6
x1=6,x2=-6
г) пустое множество
д)разделить обе стороны уравнения на о,5
х^2-2=0
x^2=2
x^2=2
x1=√2
х2=-√2
е)разделить обе части уравнения на 0,6
x+15x^2=0
x(1+15x)=0
x=0
1+15x=0
x=-1/15
x1=-1/15,x2=0