
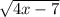 =3, возведем обе части в квадрат (чтобы избавиться от корня квадратного) и получим
=3, возведем обе части в квадрат (чтобы избавиться от корня квадратного) и получим -10x+1=25
-10x+1=25 -10x+1-25=0
-10x+1-25=0 -10x-24=0 получили квадратное уравнение, найдем дискриминант и корни
-10x-24=0 получили квадратное уравнение, найдем дискриминант и корни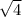 =2
=2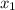 =6,
=6, 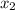 =4
=4 -3x=2x-4
-3x=2x-4 -3x-2x+4=0
-3x-2x+4=0 -5x+4=0 получили квадратное уравнение,найдем дискриминант и его корни
-5x+4=0 получили квадратное уравнение,найдем дискриминант и его корни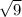 =3
=3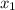 =4,
=4, 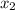 =1
=1 -3x=
-3x= +6x+9
+6x+9 -3x-
-3x- -6x-9=0, приведем подобные слагаемые и получим
-6x-9=0, приведем подобные слагаемые и получим
смотри всего имеем 6*6*6 из них нормуль 1+1+4, 1+2+3, 1+3+2, 1+4+1, 2+1+3, 2+2+2, 2+3+1, 3+1+2, 3+2+1, 4+1+1. Итого: 10 благоприятных. ответ: 10/(6*6*6)