1. (2:3):(4:5:6) = 5
2. Если a:b = c:d, то ad = bc, тогда добавим к левой и правой части ab:
ad + ab = bc + ab
a(b+d) = b(a+c)
a:b = (a+c):(b+d), что и требовалось доказать.
Пропорция a:b=(a*c):(b*d) сокращением принимает вид: 1 = c:d
То есть для верности пропорции необходимо, чтобы
либо a=b=c=d и не равны 0, либо a=c=0. В остальных случаях указанная пропорция - не верна.
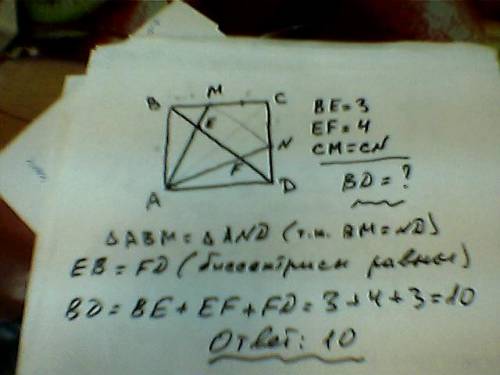
3. ответ: 10
Рисунок с решением во вложении
4. Нельзя!
Докажем от противного. Допустим можно так расставить числа. Выберем тогда четверки чисел, следующие одна за другой. Раз суммы чисел в каждой из четверок делятся на 3, значит сумму всех четверок чисел можно представить как 3*к, где к - натуральное число. Но сумма всех нат. чисел от 1 до 16 равна 136, а 136 нацело на 3 не делится. Значит мы доказали невозможность такого разбиения
a + b + c=0 (1)
a^2 + b^2 + c^2=1 (2)
a^4 + b^4 + c^4 - ?
(a + b + c)^2=0^2
a^2 + b^2 + c^2 + 2 * (ab + ac + bc) = 0
из (2) получим:
2 * (ab + ac + bc) = -1
ab + ac + bc = -1/2
(a^2 + b^2 + c^2)^2 = 1^2
(a^4 + b^4 + c^4) + 2 * (a^2*b^2 + a^2*c^2 + b^2*c^2) = 1
a^4 + b^4 + c^4 = 1 - 2 * (a^2*b^2 + a^2*c^2 + b^2*c^2) (3)
найдём (a^2*b^2 + a^2*c^2 + b^2*c^2):
ab + ac + bc = -1/2
(ab + ac + bc)^2 = 1/4
(a^2*b^2 + a^2*c^2 + b^2*c^2) + 2 * (a^2*b*c + a*b^2*c + a*b*c^2) = 1/4
a^2*b^2 + a^2*c^2 + b^2*c^2 = 1/4 - 2 * abc * (a+b+c)
Зная (1):
a^2*b^2 + a^2*c^2 + b^2*c^2 = 1/4
Вернёмся к (3):
a^4 + b^4 + c^4 = 1 - 2 * 1/4 = 1 - 1/2 = 1/2
2^-x *2^2y = 2^1
3^(3y+x) = 3^0
2^(-x+2y)= 2^1
3y+x =0
-x +2y =1
+
3y+x-x+2y =0+1
5y = 1
y =1/5
y =0.2
x = -3y
x =-3*0.2
x = -0.6